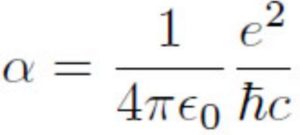Category: Mathematics

What is the fine-structure constant?

Many smart physicists wonder about it; some obsess over it; a few have gone mad. Physicists like the late Richard Feynman said that it’s not something any human can or will ever understand; it’s a rabbit-hole that quantum physicists must stand beside and peer into to do their work; but for heaven’s sake don’t rappel into its depths. No one who does has ever returned and talked sense about it.

I’m a Pontificator, not a scientist. I hope I don’t start to regret writing this essay. I hope I don’t make an ass of myself as I dare to go where angels fear to tread.

My plan is to explain a mystery of existence that can’t be explained — even to people who have math skills, which I am certain most of my readers don’t. Lack of skills should not trouble anyone, because if anyone has them, they won’t understand my explanation anyway.

My destiny is failure. I don’t care. My promise, as always, is accuracy. If people point out errors, I fix them. I write to understand; to discover and learn.

My recommendation to readers is to take a dose of whatever medicine calms their nerves; to swallow whatever stimulant might ignite electrical fires in their brains; to inhale, if necessary, doctor-prescribed drugs to amplify conscious experience and broaden their view of the cosmos. Take a trip with me; let me guide you. When we’re done, you will know nothing about the fine-structure constant except its value and a few ways curious people think about it.

Oh yes, we’re going to rappel into the depths of the rabbit-hole, I most certainly assure you, but we’ll descend into the abyss together. When we get lost (and we most certainly will) — should we fall into despair and abandon our will to fight our way back — we’ll have a good laugh; we’ll cry; we’ll fall to our knees; we’ll become hysterics; we’ll roll on the soft grass we can feel but not see; we will weep the loud belly-laugh sobs of the hopelessly confused and completely insane — always together, whenever necessary.

Isn’t getting lost with a friend what makes life worth living? Everyone gets lost eventually; it’s better when we get lost together. Getting lost with someone who doesn’t give a care; who won’t even pretend to understand the simplest things about the deep, dark places that lie miles beyond our grasp; that lie beneath our feet; that lie, in some cases, just behind our eyeballs; it’s what living large is all about.

Isn’t it?

Well, for those who fear getting lost, what follows is a map to important rooms in the rather elaborate labyrinth of this essay. Click on subheadings to wander about in the caverns of knowledge wherever you will. Don’t blame me if you miss amazing stuff.  Amazing is what hides within and between the rooms for anyone to discover who has the serenity to take their time, follow the spelunking Sherpa (me), and trust that he (me) will extricate them eventually — sane and unharmed.  

1 — Complex Numbers, Probabilities, and Vectors
2 — Elementary particles
3 — Coupling constants
4 — Irrational numbers and music 
5 — Gravity and Relativity 
6 — Fine Structure: What is it, exactly?
7 — Mystic and numerology secrets of 137
8 — Why alpha (α)?
9 — Twelve whys for alpha (α) 
10 — Deepest mystery 
11 — Summary
12 — Avoiding the rabbit hole

Anyway, relax. Don’t be nervous. The fine-structure constant is simply a number — a pure number. It has no meaning. It stands for nothing — not inches or feet or speed or weight; not anything. What can be more harmless than a number that has no meaning?

Well, most physicists think it reveals, somehow, something fundamental and complicated going on in the inner workings of atoms — dynamics that will never be observed or confirmed, because they can’t be. The world inside an atom is impossibly small; no advance in technology will ever open that world to direct observation by humans.

What physicists can observe is the frequencies of light that enormous collections of atoms emit. They use prisms and spectrographs. What they see is structure in the light where none should be. They see gaps — very small gaps inside a single band of color, for example. They call it fine structure.

The Greek letter alpha (α) is the shortcut folks use for the fine-structure constant, so they don’t have to say a lot of words. The number is the square of another number that can have (and almost always does have) two or more parts — a complex number. Complex numbers have real and imaginary parts; math people say that complex numbers are usually two dimensional; they must be drawn on a sheet of two dimensional graph paper — not on a number line, like counting numbers always are.

Don’t let me turn this essay into a math lesson; please, …no. We can’t have readers projectile vomiting or rocking to the catatonic rhythms of a panic attack. We took our medicines, didn’t we? We’re going to be fine.

I beg readers to trust; to bear with me for a few sentences more. It will do no harm. It might do good. Besides, we can get through this, together.

Like me, you, dear reader, are going to experience power and euphoria, because when people summon courage; when they trust; when they lean on one another; when — like countless others — you put your full weight on me; I will carry you. You are about to experience truth, maybe for the first time in your life. Truth, the Ancient-of-Days once said, is that golden key that unlocks our prison of fears and sets us free.

Reality is going to change; minds will change; up is going to become down; first will become last and last first. Fear will turn into exhilaration; exhilaration into joy; joy into serenity; and serenity into power. But first, we must inner-tube our way down the foamy rapids of the next ten paragraphs. Thankfully, they are short paragraphs, yes….the journey is do-able, peeps. I will guide you.

The number (3 + 4i) is a complex number. It’s two dimensional. Pick a point in the middle of a piece of graph paper and call it zero (0 + 0i). Find a pencil — hopefully one with a sharp point. Move the point 3 spaces to the right of zero; then move it up 4 spaces. Make a mark. That mark is the number (3 + 4i). Mathematicians say that the “i” next to the “4” means “imaginary.” Don’t believe it.

They didn’t know what they were talking about, when first they worked out the protocols of two-dimensional numbers. The little “i” means “up and down.” That’s all. When the little “i” isn’t there, it means side to side. What could be more simple?

Draw a line from zero (0 + 0i) to the point (3 + 4i). The point is three squares to the right and 4 squares up. Put an arrow head on the point. The line is now an arrow, which is called a vector. This particular vector measures 5 squares long (get out a ruler and measure, anyone who doesn’t believe).

The vector (arrow) makes an angle of 53° from the horizontal. Find a protractor in your child’s pencil-box and measure it, anyone who doubts. So the number can be written as (5∠53), which simply means it is a vector that is five squares long and 53° counter-clockwise from horizontal. It is the same number as (3 + 4i), which is 3 squares over and 4 squares up.

The vectors used in quantum mechanics are smaller; they are less than one unit long, because physicists draw them to compute probabilities. A probability of one is 100%; it is certainty. Nothing is certain in quantum physics; the chances of anything at all are always less than certainty; always less than one; always less than 100%.

Using simple rules, a vector that is less than one unit long can be used in the mathematics of quantum probabilities to shrink and rotate a second vector, which can shrink and rotate a third, and a fourth, and so on until the process of steps that make up a quantum event are completed. Lengths are multiplied; angles are added. The rules are that simple. The overall length of the resulting vector is called its amplitude.

Yes, other operations can be performed with complex numbers; with vectors. They have interesting properties. Multiplying and dividing by the “imaginary” i rotates vectors by 90°, for example. Click on links to learn more. Or visit the Khan Academy web-site to watch short videos. It’s not necessary to know how everything works to stumble through this article.

The likelihood that an electron will emit or absorb a photon cannot be derived from the mathematics of quantum mechanics. Neither can the force of the interaction. Both must be determined by experiment, which has revealed that the magnitude of these amplitudes is close to ten percent (.085424543… to be more exact), which is about eight-and-a-half percent.

What is surprising about this result is that when physicists multiply the amplitudes with themselves (that is, when they “square the amplitudes“) they get a one-dimensional number (called a probability density), which, in the case of photons and electrons, is equal to alpha (α), the fine-structure constant, which is .007297352… or 1 divided by 137.036… .

Get out the calculator and multiply .08524542 by itself, anyone who doesn’t believe. Divide the number “1” by 137.036 to confirm.

From the knowledge of the value of alpha (α) and other constants, the probabilities of the quantum world can be calculated; when combined with the knowledge of the vector angles, the position and momentum of electrons and photons, for example, can be described with magical accuracy — consistent with the well-known principle of uncertainty, of course, which readers can look up on Wikipedia, should they choose to get sidetracked, distracted, and hopelessly lost.

“Magical” is a good word, because these vectors aren’t real. They are made up — invented, really — designed to mimic mathematically the behavior of elementary particles studied by physicists in quantum experiments. No one knows why complex vector-math matches the experimental results so well, or even what the physical relationship of the vector-math might be (if any), which enables scientists to track and measure tiny bits of energy.

To be brutally honest, no one knows what the “tiny bits of energy” are, either. Tiny things like photons and electrons interact with measuring devices in the same ways the vector-math says they should. No one knows much more than that.

And no one knows the reasons why. Not even the late Richard Feynman knew why the methods of quantum chromodynamics (QCD) and the methods of quantum electrodynamics (QED) — which he invented and for which he won a Nobel Prize in 1965 — worked.

What is known is that the strong force of QCD is 137 times stronger than the electromagnetic force of QED — inside the center of atoms. Multiply the strong force by (α) to get the EM force.  No one knows why.

There used to be hundreds of tiny little things that behaved inexplicably during experiments. It wasn’t only tiny pieces of electricity and light. Physicists started running out of names to call them all. They decided that the mess was too complicated; they discovered that they could simplify the chaos by inventing some new rules; by imagining new particles that, according to the new rules, might never be observed; they named them quarks.

By assigning crazy attributes (like color-coded strong forces) to these quarks, they found a way to reduce the number of elementary particles to seventeen; these are the stuff that makes up the so-called Standard Model. The model contains a collection of neutrons and muons; and quarks and gluons; and thirteen other things — researchers made the list of subatomic particles shorter and a lot easier to organize and think about.

Some particles are heavy, some are not; some are force carriers; one — the Higgs — imparts mass to the rest. The irony is this: none are particles; they only seem to be because of the way we look at and measure whatever they really are. And the math is simpler when we treat the ethereal mist like a collection of particles instead of tiny bundles of vibrating momentum within an infinite continuum of no one knows what.

Physicists have developed protocols to describe them all; to predict their behavior. One thing they want to know is how forcefully and in which direction these fundamental particles move when they interact, because collisions between subatomic particles can reveal clues about their nature; about their personalities, if anyone wants to think about them that way.

The force and direction of these collisions can be quantified by using complex (often three-dimensional) numbers to work out between particles a measure during experiments of their interaction probabilities and forces, which help theorists to derive numbers to balance their equations. These balancing numbers are called coupling constants.

The fine-structure constant is one of a few such coupling constants. It is used to make predictions about what will happen when electrons and photons interact, among other things. Other coupling constants are associated with other unique particles, which have their own array of energies and interaction peculiarities; their own amplitudes and probability densities; their own values. One other example I will mention is the gravitational coupling constant.

To remove anthropological bias, physicists often set certain constants such as the speed of light (c), the reduced Planck constant (ℏ) , the fundamental force constant (e), and the Coulomb force constant (4πε) equal to “one”. Sometimes the removal of human bias in the values of the constants can help to reveal relationships that might otherwise go unnoticed.

The coupling constants for gravity and fine-structure are two examples.

  for gravity;

  for fine-structure.

These relationships pop-out of the math when extraneous constants are simplified to unity.

Despite their differences, one thing turns out to be true for all coupling constants — and it’s kind of surprising. None can be derived or worked out using either the theory or the mathematics of quantum mechanics. All of them, including the fine-structure constant, must be discovered by painstaking experiments. Experiments are the only way to discover their values.

Here’s the mind-blowing part: once a coupling constant — like the fine-structure alpha (α) — is determined, everything else starts falling into place like the pieces of a puzzle.

The fine-structure constant, like most other coupling constants, is a number that makes no sense. It can’t be derived — not from theory, at least. It appears to be the magnitude of the square of an amplitude (which is a complex, multi-dimensional number), but the fine-structure constant is itself one-dimensional; it’s a unit-less number that seems to be irrational, like the number π.

For readers who don’t quite understand, let’s just say that irrational numbers are untidy; they are unwieldy; they don’t round-off; they seem to lack the precision we’ve come to expect from numbers like the gravity constant — which astronomers round off to four or five decimal places and apply to massive objects like planets with no discernible loss in accuracy. It’s amazing to grasp that no constant in nature, not even the gravity constant, seems to be a whole number or a fraction.

Based on what scientists think they know right now, every constant in nature is irrational. It has to be this way.

Musicians know that it is impossible to accurately tune a piano using whole numbers and fractions to set the frequencies of their strings. Setting minor thirds, major thirds, fourths, fifths, and octaves based on idealized, whole-number ratios like 3:2 (musicians call this interval a fifth) makes scales sound terrible the farther one goes from middle C up or down the keyboard.

No, in a properly tuned instrument the frequencies between adjacent notes differ by the twelfth root of 2, which is 1.059463094…. . It’s an irrational number like “π” — it never ends; it can’t be written like a fraction; it isn’t a ratio of two whole numbers.

In an interval of a major fifth, for example, the G note vibrates 1.5 times faster than the C note that lies 7 half-steps (called semitones) below it. To calculate its value, take the 12th root of two and raise it to the seventh power. It’s not exactly 1.5. It just isn’t.

Get out the calculator and try it, anyone who doesn’t believe.

[Note from the Editorial Board: a musical fifth is often written as 3:2, which implies the fraction 3/2, which equals 1.5. Twelve half-notes make an octave; the starting note plus 7 half-steps make 8. Dividing these numbers by four makes 12:8 the same proportion as 3:2, right? The fraction 3/2 is a comparison of the vibrational frequencies (also of the nodes) of the strings themselves, not the number of half-tones in the interval.

However, when the first note is counted as one and flats and sharps are ignored, the five notes that remain starting with C and ending with G, for example, become the interval known as a perfect fifth. It kind of makes sense, until musicians go deeper; it gets a lot more complicated. It’s best to never let musicians do math or mathematicians do music. Anyone who does will create a mess of confusion, eight times out of twelve, if not more.]

An octave of 12 notes exactly doubles the vibrational frequency of a note like middle C, but every note in between middle C and the next higher octave is either a little flat or a little sharp. It doesn’t seem to bother anyone, and it makes playing in large groups with different instruments possible; it makes changing keys without everybody having to re-tune their instruments seem natural — it wasn’t as easy centuries ago when Mozart got his start.

The point is this:

Music sounds better when everyone plays every note a little out of tune. It’s how the universe seems to work too.

Irrationality is reality. It works just fine.

As for gravity, it works in part because space-time seems to curve and weave in the presence of super-heavy objects. No particle has ever been found that doesn’t follow the curved space-time paths that surround massive objects like our Sun.

Even particles like photons of light, which in the vacuum of space have no mass (or electric charge, for that matter) follow these curves; they bend their trajectories as they pass by heavy objects, even though they lack the mass and charge that some folks might assume they should to conduct an interaction.

Massless, charge-less photons do two things: first, they stay in their lanes — that is they follow the curved currents of space-time that exist near massive objects like a star; they fall across the gravity gradient toward these massive objects at exactly the same rate as every other particle or object in the universe would if they found themselves in the same gravitational field.

Second, light refracts in the dielectric of a field of gravity in the same way it refracts in any dialectric—like glass, for example. The deeper light falls into a gravity field, the stronger is the field’s refractive index, and the more light bends. 

Measurements of star-position shifts near the edge of our own sun helped prove that space and time are curved like Einstein said and that Isaac Newton‘s gravity equation gives accurate results only for slow moving, massive objects.

Massless photons traveling from distant stars at the speed of light deflect near our sun at twice the angle of slow-moving massive objects. The deflection of light can be accounted for by calculating the curvature of space-time near our sun and adding to it the deflection forced by the refractive index of the gravity field where the passing starlight is observed. 

In the exhilaration of observations by Eddington during the eclipse of 1919 which confirmed Einstein’s general theory, Einstein told a science reporter that space and time cannot exist in a universe devoid of matter and its flip-side equivalent, energy. People were stunned, some of them, into disbelief. Today, all physicists agree.

The coupling constants of subatomic particles don’t work the same way as gravity. No one knows why they work or where the constants come from. One thing scientists like Freeman Dyson have said: these constants don’t seem to be changing over time.

Evidence shows that these unusual constants are solid and foundational bedrocks that undergird our reality. The numbers don’t evolve. They don’t change.

Confidence comes not only from data carefully collected from ancient rocks and meteorites and analyzed by folks like Denys Wilkinson, but also from evidence uncovered by French scientists who examined the fossil-fission-reactors located at the Oklo uranium mine in Gabon in equatorial Africa. The by-products of these natural nuclear reactors of yesteryear have provided incontrovertible evidence that the value of the fine-structure constant has not changed in the last two-billion years. Click on the links to learn more.

Since this essay is supposed to describe the fine-structure constant named alpha (α), now might be a good time to ask: What is it, exactly? Does it have other unusual properties beside the coupling forces it helps define during interactions between electrons and photons? Why do smart people obsess over it?

I am going to answer these questions, and after I’ve answered them we will wrap our arms around each other and tip forward, until we lose our balance and fall into the rabbit hole. Is it possible that someone might not make it back? I suppose it is. Who is ready?

Alpha (α) (the fine-structure constant) is simply a number that is derived from a rotating vector (arrow) called an amplitude that can be thought of as having begun its rotation pointing in a negative (minus or leftward direction) from zero and having a length of .08524542…. . When the length of this vector is squared, the fine-structure constant emerges.

It’s a simple number — .007297352… or 1 / 137.036…. It has no physical significance. The number has no units (like mass, velocity, or charge) associated with it. It’s a unit-less number of one dimension derived from an experimentally discovered, multi-dimensional (complex) number called an amplitude.

We could imagine the amplitude having a third dimension that drops through the surface of the graph paper. No matter how the amplitude is oriented in space; regardless of how space itself is constructed mathematically, only the absolute length of the amplitude squared determines the value of alpha (α).

Amplitudes — and probability densities calculated from them, like alpha (α) — are abstract. The fine-structure constant alpha (α) has no physical or spatial reality whatsoever. It’s a number that makes interaction equations balance no matter what systems of units are used.

Imagine that the amplitude of an electron or photon rotates like the hand of a clock at the frequency of the photon or electron associated with it. Amplitude is a rotating, multi-dimensional number. It can’t be derived. To derive the fine structure constant alpha (α), amplitudes are measured during experiments that involve interactions between subatomic particles; always between light and electricity; that is, between photons and electrons.

I said earlier that alpha (α) can be written as the fraction “1 / 137.036…”. Once upon a time, when measurements were less precise, some thought the number was exactly 1 / 137.

The number 137 is the 33rd prime number after zero; the ancients believed that both numbers, 33 and 137, played important roles in magic and in deciphering secret messages in the Bible. The number 33 was Christ’s age at his crucifixion. It was proof, to ancient numerologists, of his divinity.

The number 137 is the value of the Hebrew word, קַבָּלָה (Kabbala), which means to receive wisdom.

In the centuries before quantum physics — during the Middle Ages  — non-scientists published a lot of speculative nonsense about these numbers. When the numbers showed up in quantum mechanics during the twentieth century, mystics raised their eyebrows. Some convinced themselves that they saw a scientific signature, a kind of proof of authenticity, written by the hand of God.

That 137 is the 33rd prime number may seem mysterious by itself. But it doesn’t begin to explain the mysterious properties of the number 33 to the mathematicians who study the theory of numbers. The following video is included for those readers who want to travel a little deeper into the abyss.

Numerology is a rabbit-hole in and of itself, at least for me. It’s a good thing that no one seems to be looking at the numbers on the right side of the decimal point of alpha (α) — .036 might unglue the too curious by half.

Read right to left (as Hebrew is), the number becomes 63 — the number of the abyss. 

I’m going to leave it there. Far be it for me to reveal more, which might drive innocents and the uninitiated into forests filled with feral lunatics.

Folks are always trying to find relationships between α and other constants like π and e. One that I find interesting is the following:

  = 

Do the math. It’s mysterious, no?

Well, it might be until someone subtracts

which brings the result even closer to the experimentally determined value of α. Somehow, mystery diminishes with added complexity, correct? Numerology can lead to peculiar thinking e times out of π.  Right?

The view today is that, yes, alpha (α) is annoyingly irrational; yet many other quantum numbers and equations depend upon it. The best known is:

.

What does it mean?

It means that the electric charge of an electron is equal to the square root of a number.

What number?

Well… it is a number that is two times the Planck constant (h); times the speed of light constant (c); times the electric constant (ε); times the fine-structure constant (α).

Why?

No one knows.

These constants (and others) show up everywhere in quantum physics. They can’t be derived from first principles or pure thought. They must be measured.

As technology improves, scientists make better measurements; the values of the constants become more precise. These constants appear in equations that are so beautiful and mysterious that they sometimes raise the hair on the back of a physicist’s head.

The equations of quantum physics tell the story about how small things that can’t be seen relate to one another; how they interact to make the world we live in possible. The values of these constants are not arbitrary. Change their values even a little, and the universe itself will pop like a bubble; it will vanish in a cosmic blip.

How can a chaotic, quantum house-of-cards depend on numbers that can’t be derived; numbers that appear to be arbitrary and divorced from any clever mathematical precision or derivation?

What is going on?

How can it be?

The inability to solve the riddles of these constants while thinking deeply about them has driven some of the most clever people on Earth to near madness — the fine-structure constant (α) is the most famous nut-cracker, because its reciprocal (137.036…) is so very close to the numerology of ancient alchemy and the kabbalistic mysteries of the Bible.

What is the number alpha (α) for? Why is it necessary? What is the big deal that has garnered the attention of the world’s smartest thinkers? Why is the number 1 / 137 so dang important during the modern age, when the mysticism of the ancient bards has been largely put aside?

Well, two reasons come immediately to mind. Physicists are adamant; if α was less than 1 / 143 or more than 1 / 131, the production of carbon inside stars would be impossible. All life we know is carbon-based. The life we know could not arise.

The second reason? If alpha (α) was less than 1 / 151 or more than 1 / 124, stars could not form. With no stars, the universe becomes a dark empty place.

Conscious life got lucky. The fine-structure constant (α) sits smack-dab in the middle of a sweet spot that makes a cosmos full of stars and life possible; perhaps inevitable.

Without mathematics, humans have no hope of understanding the universe.

Yet, here we are wrestling against all the evidence; against all the odds that the mysteries of existence will forever elude us. We cling to hope like a drowning sailor at sea, praying that the hour of rescue will soon come; we will blow our last breath in triumph; humans can understand. Everything is going to fall into place just as we always knew it would.

It might surprise some readers to learn that the number alpha (α) has a dozen explanations; a dozen interpretations; a dozen main-stream applications in quantum mechanics.

The simplest hand-wave of an explanation I’ve seen in print is that depending on ones point of view,  “α” quantifies either the coupling strength of electromagnetism or the magnitude of the electron charge. I can say that it’s more than these, much more. 

One explanation that seems reasonable on its face is that the magnetic-dipole spin of an electron must be interacting with the magnetic field that it generates as it rushes about its atom’s nucleus. This interaction produces energies which — when added to the photon energies emitted by the electrons as they hop between energy states — disrupt the electron-emitted photon frequencies slightly.

This jiggling (or hopping) of frequencies causes the fine structure in the colors seen on the screens and readouts of spectrographs — and in the bands of light which flow through the prisms that make some species of spectrographs work.

OK… it might be true. It’s possible. Nearly all physicists accept some version of this explanation.

Beyond this idea and others, there are many unexplained oddities — peculiar equations that can be written, which seem to have no relation to physics, but are mathematically beautiful.

For example: Euler’s number, “e” (not the electron charge we referred to earlier), when multiplied by the cosine of (1/α), equals 1 — or very nearly. (Make sure your calculator is set to radians, not degrees.) Why? What does it mean? No one knows.

What we do know is that Euler’s number shows up everywhere in statistics, physics, finance, and pure mathematics. For those who know math, no explanation is necessary; for those who don’t, consider clicking this link to Khan Academy, which will take you to videos that explain Euler’s number.

What about other strange appearances of alpha (α) in physics? Take a look at the following list of truths that physicists have noticed and written about; they don’t explain why, of course; indeed, they can’t; many folks wonder and yearn for deeper understanding:

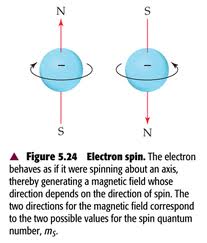
1 — One amazing property about alpha (α) is this: every electron generates a magnetic field that seems to suggest that it is rotating about its own axis like a little star. If its rotational speed is limited to the speed of light (which Einstein said was the cosmic speed limit), then the electron, if it is to generate the charge we know it has, must spin with a diameter that is 137 times larger than what we know is the diameter of a stationary electron — an electron that is at rest and not spinning like a top. Digest that. It should give pause to anyone who has ever wondered about the uncertainty principle. Physicists don’t believe that electrons spin. They don’t know where their electric charge comes from.

2 — The energy of an electron that moves through one radian of its wave process is equivalent to its mass. Multiplying this number (called the reduced Compton wavelength of the electron) by alpha (α) gives the classical (non-quantum) electron radius, which, by the way, is about 3.2 times that of a proton. The current consensus among quantum physicists is that electrons are point particles — they have no spatial dimensions that can be measured. Click on the links to learn more.

3 — The physics that lies behind the value of alpha (α) requires that the maximum number of protons that can coexist inside an atom’s nucleus must be less than 137.

Think about why. 

Protons have the same (but opposite) charge as electrons. Protons attract electrons, but repel each other. The quarks, from which protons are made, hold themselves together in protons by means of the strong force, which seems to leak out of the protons over tiny distances to pull the protons together to make the atom’s nucleus. 

The strong force is more powerful than the electromagnetic force of protons; the strong force enables protons to stick together to make an atom’s nucleus despite their electromagnetic repulsive force, which tries to push them apart.

An EM force from 137 protons inside a nucleus is enough to overwhelm the strong forces that bind the protons to blow them apart. 

Another reason for the instability of large nuclei in atoms might be — in the Bohr model of the atom, anyway — the speed that an electron hops about is approximately equal to the atomic number of the element times the fine-structure constant (alpha) times the speed of light. 

When an electron approaches velocities near the speed of light, the Lorentz transformations of Special Relativity kick in. The atom becomes less stable while the electrons take on more mass; more momentum. It makes the largest numbered elements in the periodic table unstable; they are all radioactive.

The velocity equation is V = n * α * c .  Element 118 — oganesson — presumably has some electrons that move along at 86% of the speed of light.  [ 118 * (1/137) * (3E8) ]   86% of light-speed means that relativistic properties of electrons transform to twice their rest states.

Uranium is the largest naturally occurring element; it has 92 protons. Physicists have created another 26 elements in the lab, which takes them to 118, which is oganesson.

When 137 is reached (most likely before), it will be impossible to create larger atoms. My gut says that physicists will never get to element 124 — let alone to 137 — because the Lorentz transform of the faster moving electrons grows by then to a factor of 2.3. Intuition says, it is too large. Intuition, of course, is not always the best guide to knowledge in quantum mechanics.

Plutonium, by the way — the most poisonous element known — has 94 protons; it is man-made; one isotope (the one used in bombs) has a half-life of 24,000 years. Percolating plutonium from rotting nuclear missiles will destroy all life on Earth someday; it is only a matter of time. It is impossible to stop the process, which has already started with bombs lost at sea and damage to power plants like the ones at Chernobyl and at Fukushima, Japan. (Just thought I’d mention it since we’re on the subject of electron emissions, i.e beta-radiation.)

4 — When sodium light (from certain kinds of streetlamps, for example) passes through a prism, its pure yellow-light seems to split. The dark band is difficult to see with the unaided eye; it is best observed under magnification.

The split can be measured to confirm the value of the fine-structure constant. The measurement is exact. It is this “fine-structure” that Arnold Sommerfeld noticed in 1916, which led to his nomination for the Nobel Prize; in fact Sommerfeld received eighty-four nominations for various discoveries. For some reason, he never won.

5 — The optical properties of graphene — a form of carbon used in solid-state electrical engineering — can be explained in terms of the fine-structure constant alone. No other variables or constants are needed.

6 — The gravitational force (the force of attraction) that exists between two electrons that are imagined to have masses equal to the Planck-mass is 137.036 times greater than the electrical force that tries to push the electrons apart at every distance. I thought the relationship should be the opposite until I did the math.

It turns out that the Planck-mass is huge — 2.176646 E-8 kilograms (the mass of the egg of a flea, according to a source on Wikipedia). Compared to neutrons, atoms, and molecules, flea eggs are heavy. The ratio of 137 to 1 (G force vs. e force) is hard to explain, but it seems to suggest a way to form micro-sized black holes at subatomic scales. Once black holes get started their appetites can become voracious.

The good thing is that no machine so far has the muscle to make Planck-mass morsels. Alpha (α) has slipped into the mathematics in a non-intuitive way, perhaps to warn folks that, should anyone develop and build an accelerator with the power to produce Planck-mass particles, they will have — perhaps inadvertently — designed a doomsday seed that could very well grow-up to devour Earth, if not the solar system and beyond.

7 — Alpha (α) is hidden inside the coupling constants of the electroweak theory, which unified the theories of the weak interaction and electromagnetism.

8 — The Standard Model of particle physics contains 20 or so parameters that cannot be derived; they must be experimentally discovered. One is the fine-structure constant (α), which is one of four constants that help to quantify interactions between electrons and photons.

9 — The speed of light is 137 times greater than the speed of “orbiting” electrons in hydrogen atoms. The electrons don’t actually “orbit.” They do move around in the sense of a probability distribution, though, and alpha (α) describes the ratio of their velocities to the cosmic speed limit of light. (See number 3 in this list for a description of element 118 — oganesson — and the velocity of some of its electrons.)

10 — The energy of a single photon is precisely related to the energy of repulsion between two electrons by the fine-structure constant alpha (α). Yes, it’s weird. How weird? Set the distance between two electrons equal to the wavelength of any photon. The energy of the photon will measure 137.036 times more than the repulsive force between the electrons. Here’s the problem. Everyone thinks they know that electron repulsion falls off exponentially with distance, while photon energy falls off linearly with wavelength. In these experimental snapshots, photon energy and electron repulsive energy are locked. Photons misbehave depending on how they are measured, right? The anomaly seems to have everything to do with the geometric shape of the two energy fields and how they are measured. Regardless, why “α”?

11 — The charge of an electron divided by the Planck charge — the electron charge defined by natural units, where constants like the speed of light and the gravitational constant are set equal to one — is equal to . This strange relationship is another indicator that something fundamental is going on at a very deep level, which no one has yet grasped.

The Planck relation and Planck’s law might provide additional insights for readers who want to know more.

12 — Some readers who haven’t toked too hard on their hash-pipes might remember from earlier paragraphs that the “strong force” is what holds quarks together to make protons and neutrons. It is also the force that drives protons to compactify into a solid atomic nucleus.

The strong force acts over short distances not much greater than the diameter of the atom’s nucleus itself, which is measured in femtometers. At this scale the strong force is 137 times stronger than the electromagnetic force, which is why protons are unable to push themselves apart; it is one reason why quarks are almost impossible to isolate.  Why 137?  No one has a clue.

Now, dear reader, I’m thinking that right now might be a good time to share some special knowledge — a reward for your courage and curiosity. We’ve spelunked together for quite a while, it seems. Some might think we are lost, but no one has yet complained.

Here is a warning and a promise. We are about to descend into the deepest, darkest part of the quantum cave. Will you stay with me for the final leg of the journey?  I  know the way.  Do you believe it?  Do you trust me to bring you back alive and sane?

In the Wikipedia article about α, the author writes, In natural units, commonly used in high energy physics, where ε₀ = c = h/2π = 1, the value of the fine-structure constant is:

Every quantum physicist knows the formula. In natural units e = .302822…. 

Remember that the units collapse to make “α” a dimensionless number. Dimensional units don’t go away just because the values used to calculate the final result are set equal to “1”, right? Note that the value above is calculated a little differently than that of the Planck system — where 4πε is set equal to “1”.  

As I mentioned, the value for “α” doesn’t change. It remains equal to .0073…, which is 1 / 137.036…. What puzzles physicists is, why?

What is the number 4π about? Why, when 4π is stripped away, does there remain only “α” — the mysterious number that seems to quantify a relationship of some kind between two electrons?

Well… electrons are fermions. Like protons and neutrons they have increments of 1/2 spin. What does 1/2 spin even mean?

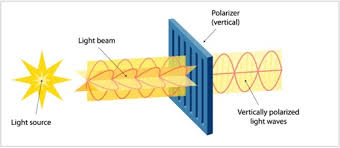
It means that under certain experimental conditions when electrons are fired through a polarized disc they project a visible interference pattern on a viewing screen. When the polarizing disc is rotated, the interference pattern on the screen changes. The pattern doesn’t return to its original configuration until the disc is rotated twice — that is, through an angle of 720°, which is 4π radians.

Since the polarizer must be spun twice, physicists reason that the electron must have 1/2 spin (intrinsically) to spin once for every two spins of the polarizer. Yes, it makes no sense. It’s crazy — until it isn’t.

What is more insane is that an irrational, dimensionless number that cannot be derived by logic or math is all that is left. We enter the abyss when we realize that this number describes the interaction of one electron and one photon of light, which is an oscillating bundle of no one knows what (electricity and magnetism, ostensibly) that has no mass and no charge.

All photons have a spin of one, which reassures folks (because it seems to make sense) until they realize that all of a photon’s energy comes from its so-called frequency, not its mass, because light has no mass in the vacuum of space. Of course, photons on Earth don’t live in the vacuum of space. When photons pass through materials like glass or the atmosphere, they disturb electrons in their wake. The electrons emit polaritons, which physicists believe add mass to photons and slow them down.

Polaritons can be thought of as light-matter waves. 

The number of electrons in materials and their oscillatory behavior in the presence of photons of many different frequencies determine the production intensity of polaritons. It seems to me that the relationship cannot be linear, which simply means that intuition cannot guide predictions about photon behavior and their accumulation of mass in materials like glass and the earth’s atmosphere. Everything must be determined by experiment.

Theories that enable verifiable predictions about photon mass and behavior might exist or be on the horizon, but I am not connected enough to know. So check it out.

Anyway… frequency is the part of Einstein’s energy equation that is always left out because, presumably, teachers feel that if they unveil the whole equation they won’t be believed — if they are believed, their students’ heads might explode. Click the link and read down a few paragraphs to explore the equation.

In the meantime, here’s the equation:

When mass is zero, energy equals the Planck constant times the frequency. It’s the energy of photons. It’s the energy of light.

Photons can and do have any frequency at all. A narrow band of their frequencies is capable of lighting up our brains, which have a strange ability to make sense of the hallucinations that flow through them.

Click on the links to get a more detailed description of these mysteries.

What do physicists think they know for sure?

When an electron hops between its quantum energy states it can emit and absorb photons of light. When a photon is detected, the measured probability amplitude associated with its emission, its direction of travel, its energy, and its position are related to the magnitude of the square of a multi-dimensional number. The scalar (α) is the probability density of a measured vector quantity called an amplitude.

When multi-dimensional amplitudes are manipulated by mathematics, terms emerge from these complex numbers, which can’t be ignored. They can be used to calculate the interference patterns in double-slit experiments, for one thing, performed by every student in freshman physics.

The square root of the fine-structure constant matches the experimentally measured magnitude of the amplitude of electron/photon interactions — a number close to .085. It means that the vector that represents the dynamic of the interaction between an electron and a photon gets “shrunk” during an interaction by almost ten percent, as Feynman liked to describe it.

Because amplitude is a complex (multi-dimensional) number with an associated phase angle or direction, it can be used to help describe the bounce of particles in directions that can be predicted within the limitations of the theory of quantum probabilities.

Square the amplitude, and a number (α) emerges — the one-dimensional, unit-less number that appears in so many important quantum equations: the fine-structure constant.

Why? It’s a mystery. It seems that few physical models that go beyond a seemingly nonsensical vision of rotating hands on a traveling clock can be conjured forth by the brightest imaginations in science to explain the why or how.

The fine-structure constant, alpha (α) — like so many other phenomenon on quantum scales — describes interactions between subatomic particles — interactions that seem to make no intuitive sense. It’s a number that is required to make the equations balance. It just does what it does. The way it is — for now, at least — is the way it is. All else is imagination and guesswork backed by some very odd math and unusual constants.

By the way (I almost forgot to mention it): α is very close to 30 times the ratio of the square of the charge of an at-rest electron divided by Planck’s reduced constant.

Anyone is welcome to confirm the calculation of what seems to be a fairly precise ratio of electron charge to Planck’s constant if they want. But what does it mean?

What does it mean?

Looking for an answer will bury the unwary forever in the rabbit hole.

I’m thinking that right now might be a good time to leave the abyss and get on with our lives. Anyone bring a flashlight?

Follow me. And please — hurry.

Billy Lee

10001001.0000100100110111001111000011111000000111111

0.00000001110111100011111