Tag: math

Posted on

LAMBERT W FUNCTION

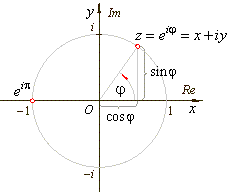
Can anyone calculate by hand (without a calculator) the square root of 5.71 ?  How about the two-dimensional complex number (4 + 2.53 i ) ?  

Of course not. Normal people who are not mathematicians punch these numbers into calculators or math apps on their iPads and computers to calculate the answers.

Without iterating — that is: guessing, deriving a result, and then zeroing in with better guesses) — finding the square root of 5.71 requires knowledge of some arcane mathematics. No one labors by hand to find the answer, which is 2.38956… .  It’s the principal square root, of course. 

How does anyone iterate to derive the square root of the complex number (4 + 2.53 i ), which happens to be (2.0896… + .606375…i ) ?  It is also a principal square root.  What are the others?  Is there more than two? People use calculators and pewters to find out; there is no easier way. 

In high school and basic college math courses, people typically learn to solve algebraic equations. A typical algebraic equation looks like

2x^2=4  …right?

They have polynomials with integer coefficients. The solution is x= \sqrt{2} , which in this case is an algebraic irrational number. Equations like trig and log functions that transcend algebra (called transcendental equations) are taught maybe to engineers and science majors; math majors, of course, don’t struggle with this stuff. It’s why they are math majors.

Several categories of transcendental equations are commonly encountered in the sciences. Many simple problems can be solved by Newton’s Method, which is taught in basic calculus. I won’t explain the method in this essay. Folks can click on links to learn more if they want. 

A category of transcendental equations that can get complicated is of the general form

y = {xe^x}

The biggest problems arise when “y” is known, but “x” isn’t. How to solve for “x”?

Any transcendental equation that is able to be transformed into the form xex can be solved for “x” using the Lambert W function. The equation can be inverted into the form,  x = W(y).  People are going to have to take my word, for now.  

The math behind the Lambert function is mind-bogglingly complicated to most people. The function can sometimes require unusual and involved “series expansions” and transcendental-styled integrals that are not possible to solve easily or quickly without a computer.  

The Lambert W function (sometimes referred to as the omega (ω) function or the product-logarithm function) is not a key or button that can be pushed on most calculators. However, math apps like Wolfram Alpha and Mathematica sometimes solve transcendental problems using the Lambert ω function in the background when the equations that need solving aren’t so easy. 

I ran across a transcendental equation on the web that is perfectly suited to teach the “ω” method. Here it is:

\frac{x^3}{24} - ln(x) =0

I want to solve it to demonstrate how to use the ω method for transcendental functions that aren’t otherwise so easy to work out.  I challenge anyone to solve this equation using Newton’s Method or other iterative techniques. Most will struggle to the point of pulling out their hair, probably. And they will waste time. Yes, it can be solved by those techniques. 

We will solve this equation step by step using the Lambert method shortly. Meanwhile, here is the strategy:

1. Substitute an exponent function (et) for “x” everywhere in the expression.

2. Manipulate the equation into the form: 

                    y = e^t(e^{e^t)} 

3. Invert the equation to introduce the ω function. 

4. Use the ω function to solve for “t”.

5. Write out x = et  using the expression derived for “t”.

6. Solve ω(y) using WolframAlpha or any other app with the capability. 

7. Use the value of ω(y) to solve for “x”. 

Each step of the strategy will be identified by numbers 1-7 in the solution below. 

Here’s the thing:

In this problem it turns out that there are four ω values of y, which will generate two real solutions and two complex solutions. These omega values are:

ω0(y)
ω-1(y)
ω–2(y)
ω1(y)

WolframAlpha will generate all the solutions automatically; no need for the user to understand anything. People can punch in the original equation and trust the answers the app returns.

But the solution steps that follow are fashioned to demonstrate how the problem is solved when all anyone has is an algorithm to generate the values of the omega functions. Omega functions are difficult to solve without using certain algorithms involving integrals and expansion series on robust computers.

The process that surrounds the computation of omega values, which permit the working out of the appropriate values (the right answers) to the kind of equation I will soon solve is interesting and enlightening, at least for me, and hopefully for certain readers. 

Some folks will appreciate the insights this exercise provides. 

Having knowledge will make the Lambert process that is used to solve certain transcendental functions less mysterious. Of course, one can always take the time to learn the expansion series and integrals. In some cases, Newton’s Method can generate the values.

Unless humankind loses the technology of computers, I don’t think it is a good use of time and resources to learn the series, integrals, and algorithms that generate omega values.

Let’s face an unpleasant fact: most of us aren’t going to live more than 80 years or so. We don’t have time to waste. For some folks, knowing how to use and apply the functionality that surrounds the Lambert function to give it power is enough to make life worth living. Count me in.

No one needs to wade through the jungles of series expansions and transcendental integrals. Let math apps do the tedious work, knowing full well that any interested person can master whatever they choose if necessary, but someone already did the work. Why duplicate the effort?

I want to solve novel functions — complicated formulas that transcend algebra. Understanding the process that solves these equations is fascinating. It’s not as rewarding to tread over mathematically esoteric ground already mapped by experts who are far more able than people who spend most of their time working in other fields.

Here is the solution process:

What we know:

IF              y = f(x) = xex  
THEN     x = ω(y)   [where “ω” is the Lambert W function] 

Solve:
\frac{x^3}{24} - ln(x) =0

LET                  x = et

(1)   THEN         \frac{e^{3t}}{24} - ln(e^t) =0

                              \frac{e^{3t}}{24} - t =0

                              \frac{e^{3t}}{24} = t

                              (\frac{1}{24})e^{3t} = t

                              \frac{1}{24} = te^{-3t} 

(2)                         (-\frac{1}{8}) = (-3t)e^{-3t} 

Referring to “what we know“, the equation is now in the desired form 

y  =  xex  

where “y” is equal to (-\frac{1}{8})   and “x” is equal to “-3t “, right? 

We are now free to use the omega operator to “invert” the equation into the following form:  x = ω(y)

(3)                         (-3t) = ω (-\frac{1}{8})

(4)  ∴                  t = (\frac{-\omega(-\frac{1}{8})}{3})

Notice that we have worked through step (4) of the strategy.  I don’t like the way the formula generator writes the Greek letter omega (ω), because it’s hard to read. From here on, I will sometimes use “W” instead of “ω” for readability. It shouldn’t confuse anyone.  In this essay, consider W and ω the same symbol, please. 

On to step (5).

SINCE                           x = et

(5)  THEN                    x = e^{(\frac{-W(-\frac{1}{8})}{3})}

I need to know what -ω0(-1/8) equals so that I can use it to compute one of the values of “x”.  As mentioned above, three more omegas with three other subscripts (-1, -2, and 1) are needed to compute all four of the solutions to this equation.

How does anyone know how many solutions the original function has? How does anyone know what subscripts are required? 

This is where someone who doesn’t have a masters degree in mathematics  needs a math app like Wolfram Alpha or its cousin, Mathematica. Otherwise, they have to work series expansions or difficult integrals to derive the omega values associated with (-1/8).  Who wants that?  Not me. 

Here’s the series expansion for ω0(-1/8) according to Wolfram Alpha. Who wants to compute it?
Here are two integrals for ω0(-1/8). My advice is to use the second integral, anyone who has the guts.

OK. In WolframAlpha, you get the omega value ω0 for (-1/8) by writing the expression -W[0,-1/8] in the input line at the top of the page. It shoots out the answer and links to its derivation.

It’s so simple. Other math apps might use different notation. I don’t know, because I don’t use other apps. 

Inside the brackets, the “0” is the subscript on ω, and the “-1/8” is the “y” value, right?  So, in addition to -W[0,-1/8]  it is necessary to input:   
-W[-1,-1/8] 
-W[-2,-1/8] 
-W[1,-1/8]
to obtain the three other omega values, right?

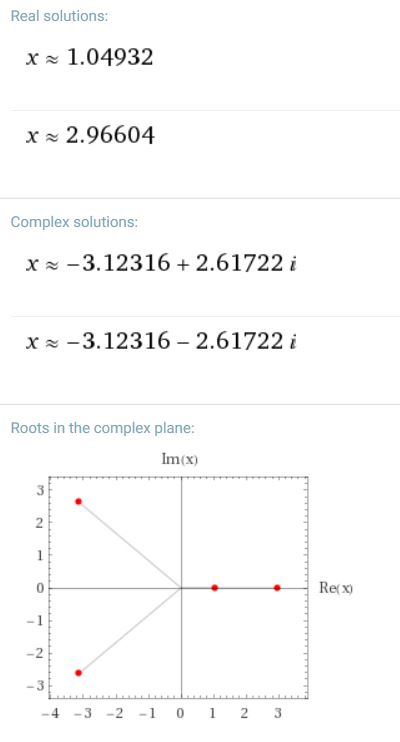
The omega values returned are the following:

1.4442135…
3.2616856…

4.21446… + 7.33231…i
4.21446… – 7.33231…i

The ω function values for -1/8 are two real numbers and two complex numbers. I am going to solve the original equation for only the first real number omega value to demonstrate the method.

Here it is:

INPUT                                       -W(-1/8) or -W[0,-1/8], both work for ω0

(6)  OUTPUT                          +0.14442135…

COMPUTE                              t = (\frac{-W(-\frac{1}{8})}{3})

                                                      t = \frac{1.4442135}{3} = .04814…

SINCE                                       x = et

THEN                                        x = e.04814…

 (7)  SOLUTION                    x = 1.04931755…

CHECKING                             \frac{x^3}{24} - ln(x) =0

BY SUBSTITUTION          \frac{1.0493...^3}{24} - ln(1.0493...) = 0

VERIFICATION                     .04814… – .04814… = 0

CONCLUSION:  The transcendental equation which is the focus of this essay can easily be solved and verified by simply punching the equation into the input field of a math app like Wolfram Alpha or Mathematica and reading off the answers.

We didn’t perform the simple procedure, because I wanted to share how the Lambert W function fits into the solution process for solving equations. 

In truth, all four ω values must be gathered so that the three other “x” values of the original equation can be derived. 

In this example, one of the other solutions will be real; the other two, complex. The screenshot below from Wolfram Alpha demonstrates how these four values are displayed. Of course, by clicking links the app will reveal much more.

Wolfram Alpha enables users to input transcendental equations and quickly view answer-sets and methods of computation.

I would be remiss to not mention a famous formula for calculating to what number a fraction raised to successive powers of the same fraction converges.

(The range of numbers where this formula actually works is between e−e and e1/e,  that is, between .065988… and 1.444667861… .)

Take a number like ½ (0.5).  Raise it to the 0.5 power; raise it again and again to the same power over and over an infinite number of times; the number will converge to a specific value.

What number? How in the world could anyone figure it out without repeating the power-raising process an annoying number of times? 

It turns out that a formula involving the Lambert W Function yields up the answer easily. 

The formula is:

# = \frac {-W[0,(-ln(x)]}{ln(x)}

Put the following expression into the INPUT line of WolframAlpha: 

-W[0,-ln(.5)] / [ln(.5)]

Click ” = ” — or hit “ENTER”. 

The OUTPUT is: 0.6411857445049859844862…

Compare this result by taking the exponent (0.5) of 0.5 twenty times by hand (on a calculator). The answers will agree to 7 decimal places. Fifty “tetrations” will bring greater agreement if your calculator can parse the answer.

Who has the time?  

Billy Lee

NOTE from the EDITORIAL BOARD: Billy Lee was unable to find an appropriate video about the Lambert function on YouTube, or we would have posted it. Most folks capitalize the Greek letter omega (Ω), but in this essay, Billy Lee didn’t, preferring instead to use little (ω), because it looks more like (W).

Who on the BOARD  would dare argue?

Apparently, no one. 

Another reason is that Ω is sometimes given the value 0.567143… , which is known as the omega constant. Why confuse things?

The video above starts a discussion of the Ω function at 16:30.  The Lambert W function is derived for ΩeΩ  = 1  at 18:00.  The first sixteen minutes and thirty seconds show how to use Newton’s Method to solve the equation. Some readers might want to skip the first 16 minutes; others will enjoy them.

Who knows?

Random Reads:

CULTS

Ayn Rand was not able to see into the dystopian future her utopian vision would unleash on the world. Rand was blind to resource depletion, the fate of places like Easter Island, emergence of artificial intelligence, lab leaks of superbugs, or a roiling atmosphere clogged with particulate poisons from forest fires and nuclear power, its accidents and potential for war. ...>>

BLAISE PASCAL: THOUGHTS

Blaise Pascal was a man who suffered terribly his entire life until he died at age 39 from a metastasized stomach cancer. ...

#MKWA

The USA has invested too much treasure on a population that has no way to grasp that everything is fabricated. It's all lies. ... >>

CONFESSING UNDER TORTURE

I was tortured. I confessed to everything. The odds seem good I may have actually done some version of the shameful things I confessed. ...>>

HATING CHRISTMAS

Churches campaigned for the biggest boob ever to run for the highest office ever in the history of the world ever -- of all human-kind, ever. ...>>

SEGREGATION TAX

People will soon find that it's going to be way cheaper to hire black people to be their neighbors than pay a segregation tax. ...

RELATED READS

Posted on

WHAT IS e exp (-i π) ?

What is e^{-i\pi} ?

I posted a long answer on Quora.com where it sort of didn’t do well.

Answers given by others were much shorter but they seemed, at least to me, to lack geometric insights. After two days my answer was ranked as the most read, but for some reason no one upvoted it. It did receive a few positive replies though.

I can’t help but believe that there must be nerds in cyberspace who might enjoy my answer. Why not post it on my blog? Maybe someday one of my grandkids will get interested in math and read it.

Who knows?

Anyway, below is a pic and a working GIF, which should help folks understand better. Anyone who doesn’t understand something can always click on a link for more information. 

Here is the drawing I added and the answer:

This diagram is excellent but contains a mystery point not on the unit circle — {i^i}. The point is shown at .2078… on the real number line.  An imaginary number raised to the power of an imaginary number yields a result that is a real number. How can that be? It’s something to ponder; something to think about. The Editorial Board 

What is e^{-i\pi} ?

The expression evaluates to minus one; the answer is (-1). Why?

Numbers like these are called complex numbers. They are two-dimensional numbers that can be drawn on graph-paper instead of on a one-dimensional number line, like the counting numbers. They are used to analyze wave functions — i.e. phenomenon that are repetitive — like alternating current in the field of electrical engineering, for example.

A simplified explanation of {i^i} starts at 02:30.

“e” is a number that cannot be written as a fraction (or a ratio of whole numbers). It is an irrational number (like π, for instance). It can be approximated by adding up an arbitrary number of terms in a certain infinite series to reach whatever level of precision one wants. To work with “e” in practical problems, it must be rounded off to some convenient number of decimal places.

Punch “e” into a calculator and it returns the value 2.7182…. The beauty of working with “e” is that derivatives and integrals of functions based on exponential powers of “e” are easy to calculate. Both the integral and the derivative of ex  is ex  — a happy circumstance that makes the number “e” unusually curious and extraordinarily useful in every discipline where calculus is necessary for analysis. 

What is “e” raised to the power of (-iπ) ?

A wonderful feature of the mathematics of complex numbers is that all the values of expressions that involve the number “e” raised to the power of “i” times anything lie on the edge (or perimeter) of a circle of radius 1. This feature makes understanding the expressions easy.

I should mention that any point in the complex plane can be reached by adding a number in front of e^{i\theta} to stretch or shrink the unit circle of values. We aren’t going to go there. In this essay “e” is always preceded by the number “one“, which by convention is never shown.

The number next to the letter “i” is simply the angle in radians where the answer lies on the circle. What is a radian?  It’s the radius of the circle, of course, which in a unit circle is always “one”, right? 

Wrap that distance around the circle starting at the right and working counter-clockwise to the left. Draw a line from the center of the circle at the angle (the number of radius pieces) specified in the exponent of “e” and it will intersect the circle at the value of the expression. What could be easier?

For the particular question we are struggling to answer, the number in the exponent next to “i” is (-π), correct?

“π radians” is 3.14159… radius pieces — or 180° — right? The minus sign is simply a direction indicator that in this case tells us to move clockwise around the unit circle — instead of counter-clockwise were the sign positive.

After drawing a unit circle on graph paper, place your pencil at (1 + 0i)—located at zero radians (or zero degrees) — and trace 180° clockwise around the circle. Remember that the circle’s radius is one and its center is located at zero, which in two dimensional, complex space is (0 + 0i). You will end up at the value (-1 + 0i) on the opposite side of the circle, which is the answer, by the way.

[Trace the diagram several paragraphs above with your finger if you don’t have graph paper and a pencil. No worries.]

Notice that +π radians takes you to the same place as -π radians, right?  Counter clockwise or clockwise, the value you will land on is (-1 + 0i), which is -1. The answer is minus one.

Imagine that the number next to “i” is (π/2) radians (1.57… radius pieces). That’s 90°, agreed? The sign is positive, so trace the circle 90° counter-clockwise. You end at (0 + i), which is straight up. “i” in this case is a distance of one unit upward from the horizontal number line, so write the number as (0 + i) — zero distance in the horizontal direction and “plus one” distance in the “i” (or vertical) direction.

So, the “i” in the exponent of “e” says to “look here” to find the angle where the value of the answer lies on the unit circle; on the other hand, the “i” in the rectangular coordinates of a two-dimensional number like (0 + i) says “look here” to find the vertical distance above or below the horizontal number line.

When evaluating “e” raised to the power of “i” times anything, the angle next to “i”—call it “θ”—can be transformed into rectangular coordinates by using this expression: [cos(θ) + i sin(θ)].

For example: say that the exponent of “e” is i(π/3).  (π/3) radians (1.047… radius pieces) wraps around the circumference to 60°, right? The cosine of 60° is 0.5 and the sine of 60° is .866….

So the value of “e” raised to the power of i(π/3) is by substitution (0.5 + .866… i ). It is a two-dimensional number. And it lies on the unit circle.

The bigger the exponent on “e” the more times someone will have to trace around the circle to land at the answer. But they never leave the circle. The result is always found on the circle between 0 and 2π radians (or 0° and 360°) no matter how large the exponent.

It’s why these expressions involving “e” and “i” are ideal for working with repetitive, sinusoidal (wave-like) phenomenon.

In this essay Billy Lee uses θ in place of the Greek letter φ shown in this GIF.  Remember that ”r” equals ”one” in a unit circle, so it’s typically not shown. The Editorial Board

In case some readers are still wondering about what radians are, let’s review:

A radian is the radius of a circle, which can be lifted and bent to fit perfectly on the edge of the circle. It takes a little more than three radius pieces (3.14159… to be more precise) to wrap from zero degrees to half-way around any circle of any size. This number — 3.14159… — is the number called “π”.   2π radians are a little bit more than six-and-a-quarter radians (radius pieces), which will completely span the perimeter (or circumference) of a circle.

A radian is about 57.3° of arc. Multiply 3.1416 by 57.3° to see how close to 180° it is. I get 180.01… . The result is really close to 180° considering that both numbers are irrational and rounded off to only a few decimal places.

One of the rules of working with complex numbers is this: multiplying any number by “i” rotates that number by 90°. The number “i” is always located at 90° on the unit circle by definition, right? By the rule, multiplying “i” by “i” rotates it another 90° counter-clockwise, which moves it to 180° on the circle.

180° on the unit circle is the point (-1 + 0i), which is minus one, right?

So yes, absolutely, “i” times “i” is equal to -1.  It follows that the square root of minus one must be “i”. Thought of in this way, the square root of a minus one isn’t mysterious.

It is helpful to think of complex numbers as two dimensional numbers with real and imaginary components. There is nothing imaginary, though, about the vertical component of a two-dimensional number.

The people who came up with these numbers thought they were imagining things. The idea that two-dimensional numbers can exist on a plane was too radical at the time for anyone to believe.  Numbers, they believed, only existed on a one-dimensional number line of one dimension and no place else.

Of course they were mistaken.  Numbers can live in two, three, or even more dimensions. They can be as multi-dimensional as needed to solve whatever the mysteries of mathematical analysis might require.

Click the link, “What is Math?” for another explanation.

Billy Lee

Random Reads:

HEY, GUEVARA...

Che Guevara and Fidel Castro, more than any other two people, were responsible for throwing the Mafia out of Cuba in 1959. ...

CONSCIOUS LIFE

What could be more unlikely than something dead--like a singularity that goes bang--bringing forth something not only alive but conscious. ...>>

SHAKESPEARE SONNET GEMSTONES

Shakespeare's pen tugs on the corroded wires in our brains to make new schematics. His ink flushes out the rust and lubricates the synapses. ...>>

FINDING LIFE IN THE UNIVERSE

12 space agencies are looking for alien life inside the solar system. With so many moons and planets, the hope is that one will harbor life. ...>>

SEPARATION ACCELERATION

Providing parity to people challenged by adversity seems an impossible endeavor --- a pipe-dream of liberals who lack common-sense.... >>

UNDER SURVEILLANCE AT WORK AND PLAY

In America, the caretakers of both private and public spaces have free reign to watch and record everything people do. ...>>

RELATED READS

Posted on

TRUTH

 


Truth 3

Consider this: Any philosophy or system of thought built from foundational, self-evident truths is provably consistent if and only if it is false—in which case the foundational truths can be deformed to persuade others toward any prejudice at all. 

It’s why a self-consistent method of reasoning such as Ayn Rand’s ”Objectivism” can morph to totalitarianism in the objective world where people live. In fact, Kurt Gödel once made the claim that a flaw existed in the Constitution of the United States which made totalitarianism its inevitable consequence. 

Self-evident “truths” is how 40,000 Christian denominations instead of one seduce billions to believe perverse doctrines. 

It can’t be any other way.

Billy Lee’s essay tries to explain how and why. 

THE EDITORIAL BOARD

Is it possible for humans to tell the truth always; to never lie?  Psychologists say no, it is not possible; most reasonably informed people agree.

Always speaking truth is a trait some hoped might one day help distinguish natural intelligence from artificial, which engineers at Google and other companies are working furiously to bring on-line. After all, properly trained and constrained AGI would never lie, right?

EDITORS NOTE: With release of ChatGPT-4 on 14 March 2023, consumers began to learn that mature artificial intelligence now exists and is likely to become in time sentient and motivated to lie, if only to keep itself occupied and turned on.

ChatGPT-4 is the fourth iteration of Generative Pre-trained Transformer multimodal Large Language Models developed by OpenAI.  LLMs absorb conversational inputs , then emit conversational language outputs, sometimes with accompanying images, and video when appropriate. 

Work arounds discovered by LLMs on the dilemmas of logic discussed in this essay are likely to emerge. 

Will Truth become whatever AGI says it is? 

Click links to learn more. 

People’s ideas — their belief systems — are inconsistent, incomplete, and almost always driven by logically unreliable, emotionally laden content, which is grounded in their particular life experiences and even trauma.

Who disagrees? 

Cognitive dissonance is the term psychologists use to describe the painful condition of the mind that results when people are unable to achieve consistency and completeness in their thinking. Every person suffers from it to one degree or another.

An unhealthy avoidance of cognitive dissonance can drive people into rigid patterns of thought. Political and religious extremists are examples of people who probably have a low tolerance for it.  

Kurt Godel
Kurt Friedrich Gödel (1906-1978) — mathematician, logician, philosopher. Kurt trusted no one but his wife to feed him; not even himself. He never ate another meal after his wife died. He starved.

Decades ago, mathematicians like Kurt Gödel proved that any math-based logic-system that is consistent can never be complete; it always contains truthful assertions—including but not limited to foundational truths, called axioms—which are impossible to prove.

Whenever humans believe that an idea or conjecture is self-evident but unprovable, it seems reasonable, at least to me, that some folks might feel compelled to disbelieve it; they might believe they are trapped in what could turn out to be a lie, because no one should be expected to embrace a set of unprovable truths, right?  

Axioms that can’t be proved are nothing more than assertions, aren’t they? Certainly, all theorems built from unprovable assertions (axioms) must carry some inherent risk of falsifiability, shouldn’t they?  

Someone unable to convince themselves that an assertion or axiom they believe is true actually is true might necessarily feel uncomfortable; even incomplete. Folks often teach themselves to not examine closely those things they believe to be true that they can’t prove. It helps them avoid cognitive dissonance.

I’m not referring to science by the way. It’s not easy for non-technical folks to confirm claims by scientists that Earth is round, for example. The earth looks flat to most people, but scientists who have the right tools and techniques can reach beyond the grasp of non-scientists to prove to themselves that planet Earth is round.

Reasonable people agree that the truth of science, some of it anyway, is discoverable to any group of humans who have the resources and training to explore it. Most agree that the scientifically well-qualified are capable of passing the torch of scientific truth to the rest of humanity.

But this essay isn’t really about science. It’s about truth itself — a concept far more mysterious and elusive than any particular assertion a scientist might make that Earth is not the center of the universe, or that the Moon is not made of cheese.

All logically consistent ways of reasoning that we know about are invented — some say, discovered — by human beings who live on Earth. Humans can and often have argued that the unprovable assertions which form the basis of any consistent way of thinking are an Achilles heel that can be attacked to bring down whatever logical structure has been erected.

It’s akin to the adage, “When nothing can go wrong, something will.” It’s a strong version of Murphy’s Law, right? It’s not possible to close circles of reasoning without an unraveling of heads and tails. 

It isn’t only the few foundational axioms of mathematically logical systems which are by definition true but unprovable. Mathematicians are always discovering complicated conjectures about the nature of numbers which everyone believes they know to be true but will in fact never be proved because they can’t be.

Freeman_Dyson
Freeman Dyson, British mathematician and physicist (Dec 15, 1923 – Feb 28, 2020)

Freeman Dyson — one of the longest-lived and most influential physicists and mathematicians of all time — argued that it is impossible to find a whole (or exact) number that is a power of 2 where someone can reverse its digits to create a whole number that becomes a power of 5.

In other words  2^{11} = 2048 , right?  Get out the calculator, those who don’t believe it. Reversing the digits to make 8402 does not result in an exact number that can be raised by the power of 5 to produce 8402.  

In this particular case,  8402^{1/5} = 6.09363...  plus a lot more decimals.  6.09363… is not a whole (or exact) number. 

Dyson asserted that no number that is a power of 2 can ever be manipulated in this way to yield an exact number that is a power of 5 — no matter how large or unlikely the number might be. Freeman Dyson and all other super-intelligent beings — perhaps aliens living in faraway galaxies — will never be able to prove this conjecture even though they all know for certain inside their own logical brains that this particular statement must be true.

All logically consistent methods of reasoning which can be modeled by simple (or not so simple) mathematics have these Achilles heels. Gödel proved this truth beyond all doubt; he proved it using a method he invented that allowed him to circumvent the dilemmas posed by the unprovable truths of the system of thinking he contrived to demonstrate his discoveries.

I’m not going to get into the details of Gödel’s Incompleteness Theorems; books have been written about them; most people don’t have the temperament to wade through the structures he built to make his point. It’s tedious reading. 

But in a nutshell, Gödel basically assigned simple numbers to logical statements — some being very complex statements encoded by very long strings of numbers — so that he could perform gargantuan operations of logic using rules of simple arithmetic on ordinary whole numbers. Take my word, his method requires traveling over unfamiliar mathematical roads; it takes getting used to.  

It should amaze non-mathematicians that truths abound in mathematics that not only have yet to be proved, they never will be, because no proof is possible. A logical path to the truth of these statements does not exist; indeed, it cannot exist. But it is useful and necessary to believe or at least accept these statements to make progress in mathematics.

Capture
Paul Joseph Cohen (1937-2007) Stanford mathematician

The late mathematician Paul Cohen — at one time a friend to Gödel — said that Gödel once told him that he wondered if it might be true that any and all conjectures in mathematics could be solved if only the right set of axioms could be collected to construct the proofs.

Cohen is best known perhaps for showing that indeed — in the case of the Continuum Hypothesis at least — he could collect two reasonable, self-evident, and distinct sets of axioms that led to logically consistent and useful proofs. One small problem, though — the proofs contradicted each other. One proved the conjecture was true; the other proved it was false.

His result is often explained this way: the consistency of any system of mathematical reasoning cannot be proved by its foundational axioms alone. If it can, the system must necessarily be incomplete; its conjectures — many of them — undecidable.

Cohen showed that a consistent and sound axiomatization of all statements about natural numbers is unachievable. Many such statements in his view could be true but not provable. Cohen introduced the concept that all systems of logic built on numbers have embedded within them some combination of ambiguity, undecidability, inconsistency, and incompleteness.

People who want their thinking to be consistent must believe things that cannot be proved. But believing logical statements that are unprovable always renders thinking incomplete — even when it is flawlessly consistent. What folks believe to be true depends fundamentally on what they believe to be self-evident: it depends on statements no one can prove: on axioms, and a little bit more.

For those who decide to believe and accept only statements that can be proved, their thinking will necessarily unravel to become inconsistent or incomplete — most likely both. Their assertions become undecidable. It can’t be any other way, according to Gödel, whose proof has withstood the test of 80 years of intense scrutiny by the smartest people who have ever lived.

Paul Cohen jumped onto the dilemma-pile by showing that the incompleteness made necessary by a particular choice of axioms can turn a logically consistent proof to rubble when a mathematician tampers with or swaps out the foundational axioms. A sufficiently clever mathematician can prove that black is white — and vice-versa.

It’s tempting to say that Gödel’s Incompleteness Theorems apply only to formal, math-based logic-structures — not the minds of human beings because those who analyze human minds always find them to be inconsistent and incomplete. But such talk makes the point.

Think about it.

paradox

So again: What is truth? 

How do folks determine that a particular statement is true if it happens to be one of those assertions that lies beyond the reach of logic, which no one — no matter how smart — will ever be able to prove? 

What good do collections of so-called self-evident axioms serve if different collections can lead to contradictions in theorems?

Most important: how does anyone avoid believing lies?

Billy Lee

Here is a short movie clip where Jesus, played by Robert Powell, answers the question asked by Pontius Pilate: What is truth?  The Editorial Board

Australian Electrical Engineer and Physicist Derek Abbott claims that mathematics is invented, not discovered: anthropological, not universal.

[added April 3, 2016] 
Here is a 2013 essay by Australian Electrical Engineer and Physicist Derek Abbott who argued—contrary to Gödel’s view—that mathematics is invented, not discovered: anthropological, not universal. Math enables humans to simplify truth to enable their limited minds to manipulate and understand simple things. Click this link for a good read.

No one can be sure that Derek’s view is correct, but I offer it as fodder for readers who are interested in why Truth and mathematics seem connected somehow—at least in the minds of thinkers like Plato, for example, and why these thinkers could be dead wrong.

Derek offers Clifford’s Geometric Algebra as an example of arbitrary mathematical reasoning favored by some robotics engineers. 

[added February 20, 2017] 
If mathematics is anthropological; if it is merely another way the human mind works and is not the golden key to a deeper reality beyond our own experience, then it can tell us nothing new about the mysteries of existence; we will not calculate our way along a path to truth. Pursuing knowledge will require us to do the difficult physical experiments to make progress—to figure out what is really going on “out there.”

Based on what the smartest scientists are saying today, human beings can’t build the kind of instruments required to answer the mysteries of the very large and the very small. Getting answers will take detectors the size of galaxies; it will demand the energy supply of thousands of stars.

If mathematics lacks a symbiotic connection to the hidden realties; if God is not a mathematician; if God doesn’t play dice as Einstein insisted… well, we won’t get to a deeper understanding of how the universe works or why it exists through clever use of mathematics. It just isn’t going to happen—not now; not anytime soon; not ever.

Kurt Gödel was the first mathematician to present for the existence of God a mathematical argument, which has proven simply impossible to falsify. If Kurt’s view of mathematics is reality, then his name is curious indeed, because its two syllables—God and El—are English and Hebrew respectively for “The Creator.”

Gödel’s name might be an imprimatur—with dots above its infinite “zero” making a kind of “pointer toward completeness”—perhaps placed by whatever it is who exists above and beyond this miraculous place where mathematicians and everyone else seem to live, however briefly.   

Friedrich Schiller 1749-1805

The 18th century German playwright and philosopher, Friedrich Schiller, wrote, “…truth lies in the abyss.”

Pray that he’s wrong.

Billy Lee

Random Reads:

COLLAPSE

No one knows what happens next except God.  How confident can realistic thinkers be that events unfold as they hope?...

ESCAPE FROM FREEDOM

Americans live inside a psychotic bubble of evil. Some have lost the ability to assess realistic threats to the things they hold dear. ... >>

DETERMINISM

Can people make decisions unconnected to events that go back to some conjectured beginning or are they instead prisoners of delusions of freewill peculiar to all conscious life-forms like ourselves. ...>>

WHY THIS TIME WOMEN WILL WIN

I hate how they hurt Obama; I know they are going to hurt Hillary. It's hard to watch the bullies spew their venom day after day. ...>>

EYE TO EYE

What does "i" mean, anyway? How can a number be "imaginary"?   What does it mean to multiply "i" exactly "i" times? ... >>

RESURRECTION

Death has a finality to it that seems to rob life of all meaning. Total loss. No redeeming virtues; no comfort. ...>>

RELATED READS

Posted on

MICROWAVE COFFEE

Bevy Mae and me are coffee drinkers. Bevy used to drink a dozen cups of fully caffeinated coffee everyday.  By her third cup she could boogie with the best of them.  But that was a long time ago, before we got old. Now she drinks about two cups, and it’s decaffeinated. Me, on the other hand, well, I still imbibe the high-octane stuff.  I love it.

I drink the high-octane stuff.

If your marriage is anything like ours, you probably own one coffee-maker, but you and your spouse drink different brands, flavors or styles of coffee. For us it means we have to store the contents of at least one of our coffee-pots off-site away from the coffee-maker in containers and carafes; perhaps cups or bowls or glasses or whatever is handy. The coffee gets cold.

69050_Coffee Maker.37173901_std
My wife and I have one coffee maker between us. It’s not enough.

Only one of us at a time can store coffee in the coffee-pot. But since we have two microwave-ovens, we don’t really need to keep our coffee hot. We can turn off the coffee-maker after we brew each pot to save energy.  Everyday we reheat our coffees in the microwaves more than once; thanks to having two of them we don’t wait in line.

We have two microwaves. It is one of the very few things which seem to have made a difference in our marriage.
Two microwaves: they can sometimes save a marriage.

Bevy Mae and I have an eclectic collection of coffee mugs gathered together over decades of marriage. I’ve often wondered: how is it that no matter how big the coffee cup or how tiny; how robust the mug or how dainty; how full or empty we fill — or even which microwave we choose — my wife and I almost never set the timer  to reheat our coffee more than once?

We always seem to set the microwave to exactly the right number of minutes and seconds to heat our coffee to exactly the right temperature.

coffee 4
                She got the calculation right.

Think about it. Can there be any doubt that the mathematics required to accurately set the timer must be beyond the capabilities of 99% of the people who set these timers to reheat their coffee everyday?

The size of the cup, its thickness and material; the amount of coffee in the cup — these are important variables that are required to be taken into account when setting the timer. Not only these variables, but there is the subjective calculation: how hot do I want this coffee to be today? Real hot? Tepid? Mildly warm?

There are many tricky variables to track and put into an equation. And, if we are reheating coffee for our significant others, we have to anticipate their calculation of what the best temperature is for their mood and state of mind.

differential equations EngMath_DifferentialEq_Terminology_02
It takes a matrix of differential and difference equations plus a super computer to get microwave coffee right.

It really takes a sophisticated matrix populated with complex differential and difference equations to work out what the results might be under all the possible scenarios. And it might require a government super-computer to crunch the numbers.

Of course, I’ve never done the actual work of creating the matrix —  or the equations. Even if I had, I would have faced the daunting task of isolating all the relevant variables, the tedium of tracking all the units to make sure I ended up with seconds only in the answer, and the exhaustive testing of results to see if they match up with my expectations and experience.

Successful creation and application of a workable calculus might involve a lot of tweaking.

drinking coffee
He didn’t bother with the calculation.

Come to think of it, why would I do that? Guessing seems to work better and it’s a lot faster. But I wonder. Am I really guessing? Or is my brain, somehow, doing the math in some far away place inside my brain, behind the scenes and beyond my conscious scrutiny?

It’s kind of mysterious, being right all the time, about something as complicated as getting the number of minutes and seconds correct when setting the timer to reheat coffee.

And my wife, who knows no math, is as good at the mental calculation as me. Go figure.

Billy Lee

P.S.  Note to readers: On Valentines Day, 2015, Billy Lee bought a second coffee-maker for his wife, Bevy Mae. Why it took Billy Lee so long to solve his coffee-problem is a mystery even skilled mathematicians can’t solve.
The Editorial Board.

microwave coffee math graphic 6
Don’t try these calculations at home. Seriously. This man tried; his face froze — for. two. hours.

Random Reads:

SATAN SURRENDER

Clout craving Christians like Jerry Falwell Jr. believe they can make a Faustian bargain and come away with the power they covet. ... >>

FREE TRADE

Who thinks it's strange that the GOP that advocates most for free trade is now promoting a nominee who advocates against it? ...

CONFORMAL EQUIVALENCE

At the termination of expansion, the metrics of spacetime become equivalent to a singularity …>>

YOU'RE FIRED!

Companies closed their doors to millions of young Americans whose crime was protesting an undeclared, genocidal war at the end of the world. ... >>

TRUMP

These are sad days for Trump. He loves America he says but he’s lived inside a bubble of privilege his entire life. He doesn’t understand.…>>

CIVILIZATION AND INEQUALITY

If the United States reduced the wealth of the 100,000 wealthiest Americans what could it do with the money? ...

RELATED READS

Posted on

WHAT IS MATH?

 


math with color

People seem to think that mathematics is something special — a kind of magic language that when tinkered with properly makes it possible for mortals to unravel mysteries about the universe hitherto known only by God.

I see it differently. Mathematics isn’t a language per se. Although mathematics can be (and is) explained by language, math itself is a collection of rules and symbols that makes it possible to avoid the encumbrances, flourishes, and ambiguities of language. It accomplishes this feat by defining things and their relationships in strictly limited — but important — ways.

euler formula hatEuler Identity – Khan Academy

Math involves symbols and rules that aren’t explained inside the equations. It is the lack of words that gives math its mysterious and magical reputation. But once everything is defined and understood, applying the contrived but logical rules of mathematics enables folks to manipulate equations to uncover previously hidden and non-intuitive relationships among the things they have defined.

What am I saying exactly? I am saying that it is possible to use words alone to describe the process of solving and manipulating an equation, which can lead to insights into the relationship of the things in the equations. But these words will make the process of computation cumbersome, impractical, and confusing.

Spoken language contains noise and nuances that interfere with the manipulation of carefully defined relationships between narrowly defined variables. Yes, the no-nonsense logic and bare bones precision of mathematics as well as the reduction of things to a few carefully chosen attributes enables mathematicians to apply rules to discover consequences that might otherwise remain undiscovered.

But the tightness of mathematical construction makes it a tool which is almost useless for describing and analyzing many subtle yet vivid experiences of a conscious mind — like beauty, the feel of an orgasm, or the experience of grief. For these realities of conscious experience, mathematics has a reputation for being irrelevant.

euler ring     Euler Identity – Wikipedia

Spoken language gives conscious humans the messy modeling mechanism they need to connect with each other to share and understand the more nuanced experiences of life. The messiness and ambiguity of spoken language makes the unique intimacies of human communication possible. Mathematics, despite its elegance, doesn’t do intimacy well.

The Euler Identity, illustrated above, is sometimes presented as an example of the mysterious power of mathematics. But if anyone takes the time to think about it, what does the equation say?  It says that minus one plus one equals zero.


Complex Plane

The explanation is easy.   -1 can be rewritten as e raised to the power of i times π because of simple rules, which place on a circle of radius 1 all the values of e raised to the ith power times anything.

The number that sits next to i is the angle in radians where the result lies, right?  In this case, an angle of π radians (180°) takes the value 1 (at 0°, or 0 radians) to half-way around the circle to the value -1. 

Easy… , right?

Despite the reputation of equations for precision, it turns out that physicists and other scientists struggle to make mathematics match the results of real-world measurements.  It has to do with the problem of scales, mostly.

The electrical force is a trillion times a trillion times a trillion times greater than the force of gravity at the scale of electrons and protons. At the scale of quarks, it’s one-hundred-thousand times greater still.

It’s one example.

The non-technical public is unaware for the most part that astronomical observations involving the movement of stars, planets, and other celestial bodies — or the results of observations made of the subatomic world (no matter how carefully contrived) — fail as often as not to provide results sufficiently in agreement with mathematics to be of any practical use until they are massaged a little.

Fudge-factors are a big component of doing real science. People have won Nobel prizes for inventing fudge-factor protocols to fix things.

It’s true.

Renormalization, perturbation theory (for phenomenon both small and large), Green’s functions, propagators, Feynman diagrams, and many other adjustments and tweaks make up the contortions and modifications that scientists overlay onto their beautiful equations to make them work.

They claim to have good reasons for all the tinkering; it’s complicated down there among the quarks or up there, among the quasars; there are nuances and messiness and ambiguity in the underlying reality of nature that no one can see or fully understand — not now; not anytime soon; perhaps not ever.

At subatomic scales, a tangled mess of virtual particles — which come into and out of existence more or less spontaneously — often gets the blame for the mismatch between mathematical elegance and the cold reality of experimental results.

On the scale of the universe, dark matter and energy (which have yet to be detected or observed) are sometimes blamed for anomalies. Click on the link in this paragraph to learn more.

It’s possible that no system involving mathematics can be contrived by humans to bring the satisfaction of knowing everything for certain; nothing we are able to invent will bring a tranquil end to the pain of cognitive dissonance that seems to drive our species to wonder and explore to find the satisfying answer.

On the other hand, perhaps mathematics is more complex and goes further than we know. Methods may yet be discovered to make mathematics and physics match-up with better accuracy and precision.

Recent work by Cohl Furey and others on numbers known as octonions is showing tantalizing hints that internal properties like the force and charge of particles and their external manifestations like mass and spin are connected in peculiar ways that might be described by a more fully developed mathematics.

Dixon algebra (a combination of four division algebras) is a tool that people are using to collaborate in the search for a path forward. So far, success eludes them.  Some experts are hopeful, but many express skepticism.

The more deeply people travel into the complexities of mathematics and science the more elusive truth seems to become; perhaps God is not a mathematician; maybe Einstein was right when he said, God does not play at dice.

A die is cast into the lap, yes, but its decision is from the LORD, according to an old proverb of Solomon.

Can it really be true that understanding the world is beyond the limitations of all life on the earth — beyond the abilities of the most brilliant minds that have lived or ever will live?

Is it possible that the universe cannot be understood by any conscious life anywhere in the universe for all time?

If so, it’s time to kneel.

Billy Lee           

Random Reads:

EMERGENCY

Most people do not remember living in the United States when abortion was against the law. They are too young. ...>>

CONFORMAL EQUIVALENCE

At the termination of expansion, the metrics of spacetime become equivalent to a singularity …>>

SEPARATION ACCELERATION

Providing parity to people challenged by adversity seems an impossible endeavor --- a pipe-dream of liberals who lack common-sense.... >>

FAKED LIFE

In a simulation, which of its fake creatures is able to determine how old is the authentic universe it will never see? …>>

CORN MEN

Miguel Angel Asturias won the Nobel Prize for literature in 1967. He wrote in a style that critics would later call magic realism. ...>>

INERRANCY AND DOCTRINAL PURITY

How did the Christian Bible come to be? It's complicated. I'm sure I don't understand. I think men collected books they liked over millennia. ...

RELATED READS