Tag: Particle spin

UPDATE: 18 December 2022:  Royal Swedish Academy of Sciences on 4 October 2022 awarded the Nobel Prize in Physics to: 

Alain Aspect
Institut d’Optique Graduate School – Université Paris-
Saclay and École Polytechnique, Palaiseau, France

John F. Clauser
J.F. Clauser & Assoc., Walnut Creek, CA, USA

Anton Zeilinger
University of Vienna, Austria

“for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science”

UPDATE: September 5, 2019:  I stumbled across this research published in NATURE during December 2011, where scientists reported entanglement of vibrational patterns in separated diamond crystals large enough to be viewed without magnification. Nature doi:10.1038/nature.2011.9532

UPDATE: May 8, 2018: This video from PBS Digital Studios is the best yet. Click the PBS link to view the latest experimental results involving quantum mechanics, entanglement, and their non-intuitive mysteries. The video is a little advanced and fast paced; beginners might want to start with this link.

UPDATE: June 17, 2016:   Ali Sundermier published a description of quantum entanglement for non-scientists. Here is the link.

Another beginner’s overview of quantum mechanics by Cathal O’Connell is in this link.

UPDATE: February 4, 2016:  Here is a link to the August 2015 article in Nature, which makes the claim that the last testable loophole in Bell’s Theorem has been closed by experiments conducted by Dutch scientists. Conclusion: quantum entanglement is real.

UPDATE: Nov. 14, 2014:    David Kaiser proposed an experiment to determine Is Quantum Entanglement Real?  Click the link to redirect to the Sunday Review, New York Times article. It’s a non-technical explanation of some of the science related to Bell’s Theorem. 

John Stewart Bell‘s Theorem of 1964 followed naturally from the proof of an inequality he fashioned (now named after him), which showed that quantum particle behavior violated logic.

It is the most profound discovery in all science, ever, according to Henry Stapp—retired from Lawrence Berkeley National Laboratory and former associate of Wolfgang Pauli and Werner Heisenberg. Other physicists like Richard Feynman said Bell simply stated the obvious.

Here is an analogy I hope gives some idea of what is observed in quantum experiments that violate Bell’s Inequality: Imagine two black tennis balls—let them represent atomic particles like electrons or photons or molecules as big as buckyballs.

The tennis balls are created in such a way that they become entangled—they share properties and destinies. They share identical color and shape.  [Entangled particles called fermions display opposite properties, as required by the Pauli exclusion principle.]

Imagine that whatever one tennis ball does, so does the other; whatever happens to one tennis ball happens to the other, instantly it turns out. The two tennis balls (the quantum particles) are entangled.

[For now, don’t worry about how particles get entangled in nature or how scientists produce them.  Entanglement is pervasive in nature and easily performed in labs.]

According to optical and quantum experimentalist Mark John Fernee of Queensland, Australia, ”Entanglement is ubiquitous. In fact, it’s the primary problem with quantum computers. The natural tendency of a qubit in a quantum computer is to entangle with the environment. Unwanted entanglement represents information loss, or decoherence. Everything naturally becomes entangled. The goal of various quantum technologies is to isolate entangled states and control their evolution, rather than let them do their own thing.”

In nature, all atoms that have electron shells with more than one electron have entangled electrons. Entangled atomic particles are now thought to play important roles in many previously not understood biological processes like photosynthesis, cell enzyme metabolism, animal migration, metamorphosis, and olfactory sensing. There are several ways to entangle more than a half-dozen atomic particles in experiments.

Imagine particles shot like tennis balls from cannons in opposite directions. Any measurement (or disturbance) made on a ball going left will have the same effect on an entangled ball traveling to the right.

So, if a test on a left-side ball allows it to pass through a color-detector, then its entangled twin can be thought to have passed through a color-detector on the right with the same result. If a ball on the left goes through the color-detector, then so will the entangled ball on the right, whether or not the color test is performed on it. If the ball on the left doesn’t go through, then neither did the ball on the right. It’s what it means to be entangled.

Now imagine that cannons shoot thousands of pairs of entangled tennis balls in opposite directions, to the left and right. The black detector on the left is calibrated to pass half of the black balls. When looking for tennis balls coming through, observers always see black balls but only the half that get through. 

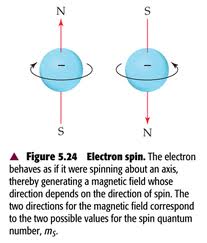
Spin describes a particle property of quantum objects like electrons — in the same way color or roundness describe tennis balls. The property is confusing, because no one believes electrons (or any other quantum objects) actually spin. The math of spin is underpinned by the complex-mathematics of spinors, which transform spin arrows into multi-dimensional objects not easy to visualize or illustrate. Look for an explanation of how spin is observed in the laboratory later in the essay. Click links for more insight.

Now, imagine performing a test for roundness on the balls shot to the right. The test is performed after the black test on the left, but before any signal or light has time to travel to the balls on the right. The balls going right don’t (and can’t) learn what the detector on the left observed. The roundness-detector is set to allow three-fourths of all round tennis balls through.

When round balls on the right are counted, three-eighths of them are passing through the roundness-detector, not three-fourths. Folks might speculate that the roundness-detector is acting on only the half of the balls that passed through the color-detector on the left. And they would be right.

These balls share the same destinies, right? Apparently, the balls on the right learned instantly which of their entangled twins the color-detector on the left allowed to pass through, despite all efforts to prevent it.

So now do the math. One-half (the fraction of the black balls that passed through the left-side color-detector) multiplied by three-fourths (the fraction calibrated to pass through the right-side roundness-detector) equals three-eighths. That’s what is seen on the right — three-eighths of the round, black tennis balls pass through the right-side roundness-detector during this fictionalized and simplified experiment.

According to Bell’s Inequality, twice as many balls should pass through the right-side detector (three-fourths instead of three-eighths). Under the rules of classical physics (which includes relativity), communication between particles cannot exceed the speed of light.

There is no way the balls on the right can know if their entangled twins made it through the color detector on the left. The experiment is set up so that the right-side balls do not have time to receive a signal from the left-side. The same limitation applies to the detectors.

The question scientists have asked is: how can these balls (quantum particles) — separated by large distances — know and react instantaneously to what is happening to their entangled twins? What about the speed limit of light? Instantaneous exchange of information is not possible, according to Einstein.

The French quantum physicist, Alain Aspect, suggested his way of thinking about it in the science journal, Nature (March 19, 1999).

He wrote: The experimental violation of Bell’s inequalities confirms that a pair of entangled photons separated by hundreds of meters must be considered a single non-separable object — it is impossible to assign local physical reality to each photon.

Of course, the single non-separable object can’t have a length of hundreds of meters, either. It must have zero length for instantaneous communication between its endpoints. But it is well established by the distant separation of detectors in experiments done in labs around the world that the length of this non-separable quantum object can be arbitrarily long; it can span the universe.

When calculating experimental results, it’s as if a dimension (in this case, distance or length) has gone missing. It’s eerily similar to the holographic effect of a black hole where the three-dimensional information that lives inside the event-horizon is carried on its two-dimensional surface. (See the technical comment included at the end of the essay.)

Another way physicists have wrestled with the violations of Bell’s Inequality is by postulating the concept of superposition. Superposition is a concept that flows naturally from the linear algebra used to do the calculations, which suggests that quantum particles exist in all their possible states and locations at the same time until they are measured.

Measurement forces wave-particles to “collapse” into one particular state, like a definite position. But some physicists, like Roger Penrose, have asked: how do all the super-positioned particles and states that weren’t measured know instantaneously to disappear?

Superposition, a fundamental principle of quantum mechanics, has become yet another topic physicists puzzle over. They agree on the math of superposition and the wave-particle collapse during measurement but don’t agree on what a measurement is or the nature of the underlying reality. Many, like Richard Feynman, believe the underlying reality is probably unknowable.

Quantum behavior is non-intuitive and mysterious. It violates the traditional ideas of what makes sense. As soon as certainty is established for one measurement, other measurements, made earlier, become uncertain.

It’s like a game of whack-a-mole. The location of the mole whacked with a mallet becomes certain as soon as it is struck, but the other moles scurry away only to pop up and down in random holes so fast that no one is sure where or when they really are.

Physicists have yet to explain the many quantum phenomena encountered in their labs except to throw-up their hands to say — paraphrasing Feynman — it is the way it is, and the way it is, well, the experiments make it obvious.

But it’s not obvious, at least not to me and, apparently, many others more knowledgeable than myself. Violations of Bell’s Inequality confound people’s understanding of quantum mechanics and the world in which it lives. A consequence has been that at least a few scientists seem ready to believe that one, perhaps two, or maybe all four, of the following statements are false:

1) logic is reliable and enables clear thinking about all physical phenomenon;

2) the universe exists independently of any conscious observer;

3) information does not travel faster than light.

4) a model can be imagined to explain quantum phenomenon.

I feel wonder whenever the idea sinks into my mind that at least one of these four seemingly self-evident and presumably true statements could be false — possibly all four — because repeated quantum experiments suggest they must be. Why isn’t more said about it on TV and radio?

The reason could be that the terrain of quantum physics is unfamiliar territory for a lot of folks. Unless one is a graduate student in physics — well, many scientists don’t think non-physicists can even grasp the concepts. They might be right.

So, a lot is being said, all right, but it’s being said behind the closed doors of physics labs around the world. It is being written about in opaque professional journals with expensive subscription fees.

The subtleties of quantum theory don’t seem to suit the aesthetics of contemporary public media, so little information gets shared with ordinary people. Despite the efforts of enthusiastic scientists — like Brian Cox, Sean M. Carroll, Neil deGrasse Tyson and Brian Greene — to serve up tasty, digestible, bite-size chunks of quantum mechanics to the public, viewer ratings sometimes fall flat.

When physicists say something strange is happening in quantum experiments that can’t be explained by traditional methods, doesn’t it deserve people’s attention? Doesn’t everyone want to try to understand what is going on and strive for insights?  I’m not a physicist and never will be, but I want to know.

Even me — a mere science-hobbyist who designed machinery back in the day — wants to know. I want to understand. What is it that will make sense of the universe and the quantum realm in which it rests?  It seems, sometimes, that a satisfying answer is always just outside my grasp.

Here is a concise statement of Bell’s Theorem from the article in Wikipedia — modified to make it easier to understand: No physical theory about the nature of quantum particles which ignores instantaneous action-at-a-distance can ever reproduce all the predictions about quantum behavior discovered in experiments.

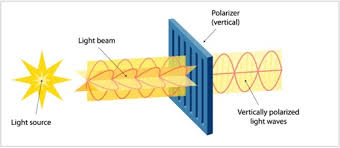
To understand the experiments that led to the unsettling knowledge that quantum mechanics — as useful and predictive as it is — does indeed violate Bell’s proven Inequality, it is helpful not only to have a solid background in mathematics but also to understand ideas involving the polarization of light and — when applied to quantum objects like electrons and other sub-atomic particles — the idea of spin.  Taken together, these concepts are somewhat analogous to the properties of color and roundness in the imaginary experiment described above.

This essay is probably not the best place to explain wave polarization and particle spin, because the explanation takes up space, and I don’t understand the concepts all that well, anyway.  (No one does.)

But, basically, it’s like this: if a beam of electrons, for example, is split into two and then recombined on a display screen, an interference pattern presents itself. If one of the beams was first passed through a polarizer, and if experimenters then rotate the polarizer a full turn (that is, 360°), the interference pattern on the screen will reverse itself.  If the polarizer-filter is rotated another full turn, the interference pattern will reverse again to what it was at the start of the experiment.

So, it takes two spins of the polarizer-filter to get back the original interference pattern on the display screen — which means the electrons themselves must have an intrinsic “one-half” spin. All so-called matter particles like electrons, protons, and neutrons (called fermions) have one-half spin.

Yes, it’s weird. Anyway, people can read-up on the latest ideas by clicking this link. It’s fun. For people familiar with QM (quantum mechanics), a technical note is included in the comments section below.

Otherwise, my analogy is useful enough, probably. In actual experiments, physicists measure more than two properties, I’m told. Most common are angular momentum vectors, which are called spin orientations. Think of these properties as color, shape, and hardness to make them seem more familiar — as long as no one forgets that each quality is binary; color is white or black; shape is round or square; hardness is soft or hard.

Spin orientations are binary too — the vectors point in one of two possible directions. It should be remembered that each entangled particle in a pair of fermions always has at least one property that measures opposite to that of its entangled partner.

The earlier analogy might be improved by imagining pairs of entangled tennis balls where one ball is black, the other white; one is round, the other square; add a third quality where one ball is hard, the other soft. Most important, the shape and color and hardness of the balls are imparted by the detectors themselves during measurement, not before.

Before measurement, concepts like color or shape (or spin or polarity) can have no meaning; the balls carry every possible color and shape (and hardness) but don’t take on and display any of these qualities until a measurement is made. Experimental verification of these realities keep some quantum physicists awake at night wondering, they say.

Anyway, my earlier, simpler analogy gets the main ideas across, hopefully. And a couple of the nuances of entanglement can be found within it. I’ve added an easy to understand description of Bell’s Inequality and what it means to the end of the essay.

Here are two additional links with more depth: CHSH Inequality; Bell Test Experiments.

In the meantime, scientists at the Austrian Academy of Sciences in Vienna recently demonstrated that entanglement can be used as a tool to photograph delicate objects that would otherwise be disturbed or damaged by high energy photons (light). They entangled photons of different energies (different colors).

They took photographs of objects using low energy photons but sent their higher energy entangled twins to the camera where their higher energies enabled them to be recorded. New technologies involving the strange behavior of quantum particles are in development and promise to transform the world in coming decades.

Perhaps entanglement will provide a path to faster-than-light communication, which is necessary to signal distant space-craft in real time. Most scientists say, no, it can’t be done, but ways to engineer around the difficulties are likely to be developed; technology may soon become available to create an illusion of instantaneous communication that is actually useful. Click on the link in this paragraph to learn more.

Non-scientists don’t have to know everything about the individual trees to know they are walking in a quantum forest. One reason for writing this essay is to encourage people to think and wonder about the forest and what it means to live in and experience it.

The truth is, the trees (particles at atomic scales) in the quantum forest seem to violate some of the rules of the forest (classical physics). They have a spooky quality, as Einstein famously put it.

Trees that aren’t there when no one is looking suddenly appear when someone is looking. Trees growing in one place seem to be growing in other places no one expected. A tree blows one way in the wind, and someone notices a tree at the other end of the forest — where there is no wind — blowing in the opposite direction. As of right now, no one has offered an explanation that doesn’t seem to lead to paradoxes and contradictions when examined by specialists.

John Stewart Bell proved that the trees in the quantum forest violate the laws of nature and logic. It makes me wonder whether anyone will ever know anything at all that they can fully trust about the fundamental, underlying essence of reality.

Some scientists, like Henry Stapp (now retired), have proposed that brains enable processes like choice and experiences like consciousness through the mechanism of quantum interactions. Stuart Hameroff and Roger Penrose have proposed a quantum mechanism for consciousness they call Orch Or.

Others, like Wolfgang Pauli and C. G. Jung, have gone further — asking, when they were alive, if the non-causal coordination of some process resembling what is today called entanglement might provide an explanation for the seeming synchronicity of some psychic processes — an arena of inquiry a few governments are rumored to have already incorporated (to great effect) into their intelligence gathering tool kits.

In a future essay I hope to speculate about how quantum processes like entanglement might or might not influence human thought, intuition, and consciousness.

Billy Lee

P.S.  A simplified version of Bell’s Inequality might say that for things described by traits A, B, and C, it is always true that A, not B; plus B, not C; is greater than or equal to: A, not C.  

When applied to a room full of people, the inequality might read as follows: tall, not male; plus male, not blonde; is greater than or equal to: tall, not blonde.

Said more simply: tall females and dark haired men will always number more than or equal to the number of tall people with dark hair. 

People have tried every collection of traits and quantities imaginable. The inequality is always true, never false; except for quantum objects.

One way to think about it: all the ”not” quantities are, in some sense, uncertain in quantum experiments, which wrecks the inequality. That is to say, as soon as ”A” is measured (for example) ,”not B” becomes uncertain. When ”not B” is measured, ”A” becomes uncertain.

The introduction of uncertainties into quantities that were — before measurement — seemingly fixed and certain doesn’t occur in non-quantum collections where individual objects are big enough to make uncertainties not noticeable. The inability to measure both the position and velocity of small things with high precision is called the uncertainty principle and is fundamental to physics. No advancement in the technology of measurement will ever overcome it.

Uncertainty is believed to be an underlying reality of nature. It runs counter to the desire humans have for complete and certain knowledge; it is a thirst that can never be quenched.

But what’s really strange: when working with entangled particles, certainty about one particle implies certainty about its entangled twin; predicted experimental results are precise and never fail.

Stranger still, once entangled quantum particles are measured, the results, though certain, change from those expected by classical theory to those predicted by quantum mechanics. They violate Bell’s Inequality and the common sense of humans about how things should work. 

Worse: Bell’s Theorem seems to imply that no one will ever be able to construct a physical model of quantum mechanics to explain the results of quantum experiments.  No ”hidden variables” exist which, if anyone knew them, would explain everything. 

Another way to say it is this: the underlying reality of quantum mechanics is unknowable.  [A technical comment about the mystery of QM is included in the comments section.]

Billy Lee