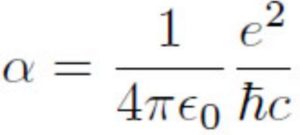quantum physics Archives - The Billy Lee Pontificator

April 3, 2021June 8, 2023

GENERAL & SPECIAL RELATIVITY

Since Einstein said that E=mc² , why does a massless photon have energy?

Someone asked a similar question on Quora. My answer garnered nearly a million views and many dozens of comments. It gave me an opportunity to gather thoughts on a subject that has puzzled folks for decades.

Of course, I’m a pontificator, not a scientist. I got advice from working physicists and incorporated what they taught me.

One thing I learned from science writer Jim Baggott is that Einstein first published his famous equation in this form:

M = $\frac{E }{ C^2}$

When written this way, it becomes clear that anyone who knows the total energy of anything can calculate in principle its total mass.

Einstein knew nothing at all about the Higgs field but today physicists agree that the mass it creates is less than 5% of what mass they have discovered.

In fact, nearly 99% of the mass of a single proton is derived from the energy of “massless” gluons that constrain its two up-quarks and one down-quark. Gluons are bosons which don’t interact with the Higgs field; quarks, which are fermions, do.

In the end, it’s all about energy, which it turns out is equivalent to mass, which according to Baggott is what quantum fields do. Quantum fields like the Higgs field make mass. Perhaps the electromagnetic field — which makes photons — does the same.

Here is Einstein’s equation for energy:

$E^{2}=\left ( mc^{2} \right )^{2} +\left (pc \right )^{2}$

Since

$p=\frac{hf}{c}$

and

$m=\frac{hf}{c^2}$

it follows that it might be reasonable to imagine that photons have both internal mass and inertial mass, which causes Einstein’s equation for energy to give the following result:

$E=\sqrt2 ({hf})$

All that is left is to divide by c² to get mass, right?

$m=\sqrt2 (\frac{hf}{c^2})$

Most folks think the internal mass of a photon is zero. Period. End of story. They use the two mass and momentum terms in Einstein’s equation to calculate total energy of massive objects, yes, but photons, they insist, lack internal mass. They lack the internal fermionic structures associated with all massive particles.

Photons do have inertial energy proportional to their critical frequency though, which suggests that they possess perhaps equivalent inertial mass, which drives the photoelectric effect.

When physicists take the energy measure of photons, they drop the mass term in Einstein’s equation. They set mass to zero and cancel out the first term, mc². It leaves the second term — pc— which for photons simplifies to hf, inertial energy correlated to frequency, right? Energy can be measured in eVs, electron-volts, which are also units of mass.

If photons have internal energy, their total energy in the universe is undervalued by 1.414 (the square root of 2). Accounting for this added mass reduces the Cosmic energy deficit to near zero.

PHOTON MASS

I should add that overestimating mass and disrupting popular models of the Cosmos is something most scientists think is a bad idea.

The gluon is the only other massless particle currently in the standard model, but it has never been observed as a free particle. All gluons are buried inside hadrons. It is their binding energy in quarks that makes as much as 99% of the measured mass of protons and neutrons.

So, there is precedent to possibly reevaluate mass equivalence of photons.

Some readers might wonder about the massless graviton. This particle is theorized to exist, yes, but has not been observed or added to the Standard Model. The same is true for dark matter and dark energy — no physical evidence; not added to the Model.

It doesn’t mean dark energy and matter don’t exist. Cosmologists see way too much gravity everywhere they look. The problem is they can’t explain exactly what is causing it.

As for my answer to the original question published on Quora, it was as accurate as my limited experience could make at the time, but the subject is controversial and several issues are not yet settled, even by experts. Some disputes might never be settled.

Who knows?

Not me. I’m a pontificator, right?

What follows is a version of the answer:

You might be mistaken about energy.

According to the complete statement of Einstein’s most well-known equation, energy content is a combination of a particle’s mass and its momentum. The equation you cite is abbreviated. It is a simplified version that is missing a term.

Einstein’s complete equation is strangely analogous to Pythagoras’s geometry of right-triangles. When anyone thinks about it though, aren’t the frequencies of light at right angles to its propagation? Light waves are transverse, right?

Here is a more complete version of Einstein’s equation:

$E^{2}=+\left ( mc^{2} \right )^{2} + \left (pc \right )^{2}$

—where m is internal mass and ρ is momentum. Internal mass is often referred to as “rest mass” because it is invariant in all reference frames and unchanged by velocity or acceleration. Momentum is inertial energy measured in equivalent mass units called electron volts (eVs).

Massless particles like photons have momentum that is correlated to their wavelengths (or frequencies). It’s their frequencies that give massless particles like photons their energy content. So without (rest) internal mass the equation becomes:

E=ρc

—where $p=\frac{hf}{c}$ for massless photons.

So, E = hf

[“h” is Planck’s constant. “f” is frequency. “c” is light speed.]

Of course, in classical Newtonian physics ρ = mc. The mass term is critical.

Screen shot from Khan Academy showing derivation of photon momentum. Typed mark-ups by me show mass equivalence when ρ is set equal to mc. When mc = hf/c, then m = hf/c*c, right? Click the pic for a better view in a new window.

On the other hand, in quantum mechanics the total mass of photons cannot be zero either—photon internal mass is set equal to zero and eliminated. Inertial energy based on the photon’s critical frequency (the 2nd term in Einstein’s equation) becomes its equivalent mass. I’m not sure everyone agrees.

The beauty created by setting photon rest-mass (internal energy) to zero is it transforms the maths of relativity and quantum mechanics into structures that seem to be consistent and complete — able, one hopes, to meld into theories of everything; TOEs, if you like. The problem, of course, is that the convention of setting to zero leaves thrashing in its wake 95% of the mass and energy which “other” stories claim is hidden unseen “out there” within and around galaxies to move them faster than they ought.

The Abraham-Minkowski controversy seems to touch the argument. Click the link and scroll to the end of the article to learn how many things are disputed, not known, or unexplained. The science is not settled, although several physicists claim that the controversy is resolved by postulating an interaction inside dielectrics (like glass) of photons with electron-generated polaritons.

NOTE BY EDITORS: On 18 April 2021 a writer massively abbreviated and modified the article in Wikipedia on the A-M controversy. The writer deleted the entire list of disputed claims. Please click the link in this sentence to review a list of unsolved problems in modern physics. Photon mass inside dielectrics isn’t on the list.

The permittivity of “empty“ space (called the electric constant) qualifies as a dielectric, does it not? Isn’t space itself—with its Maxwell-assigned permeability (the magnetic constant) and permittivity (electric constant)—a dielectric?

Arthur Eddington wrote in chapter 6 of his book Space Time and Gravitation (read pages 107-109) that the dielectrics of space around the Sun increase proportionally with the intensity of the gravitational field. Light waves closest to the sun slow down more, which pulls the wavefront that lies farther out to deflect still more to catch up. Like glass, gravity refracts light.

Light falls into the Sun like any solid rock, but refraction adds to light’s “Newtonian” deflection to give Einstein’s predicted result. Unlike slow rocks, light travels fast enough to avoid capture by the sun.

It’s not clear to me how many physicists agree with Eddington, but then again, it’s not obvious whether humanoids are able to visualize reality. It’s one thing to write equations and symbolic algorithms that match well with observations. It’s quite another to acquire a natural intuition for what might be true.

Empty space isn’t empty, right?

As for the Abraham-Minkowski dispute: how important might it be to decisively resolve ambiguities concerning photon mass?

Perhaps the dispute is swept under a rug because disagreements about something as fundamental as photon mass mean that physicists might know less than they let on. The controversy seems to me at least to have the potential to crash the tidy physics of light and mass built by hard work and much history.

Isn’t it better to pretend everything is just fine until physicists finally agree that everything really is?

Maybe the subject involves some aspect of national security which requires obfuscation. It wouldn’t be the first time.

What I think can be safely said is that momentum and mass of quantum objects seem to have no meaning until they are brought into existence by measurements. The math looks like nothing we know; sometimes physicists use the results as mathematical operators that don’t commute the way some might think they should.

PHOTONS AND GRAVITY

I reviewed the math. I saw the term that makes the deflection difference (it’s really there) but did not understand enough at the time to tease out a satisfying reason why photons seem to bend nearly twice more in a gravitational field than early acolytes of Newton conjectured. I guess I like Eddington’s explanation best.

According to Wikipedia, Einstein’s theory approximates the deflection to be:

$\frac{4GM}{(c^2)b}$

“b” is the distance of a photon’s closest approach to a gravitational object like our Sun.

Here’s some guesses I made before reading Eddington:

Maybe light deeply buried in a gravity field near a star like the Sun will experience the flow of time more slowly—it’s an effect common to all objects in a gravity field; it affects all objects the same way and is unaffected by their mass or lack of it.

It might have something to do with Schwarzchild geodesics. The geodesics of spacetime paths are longer and more curved in a gravity field than what anyone might expect from a simple application of Newton’s force law, which is oblivious to the spacetime metrics of Einstein.

Schwarzchild metrics help to explain the “gravitational lensing” of faraway objects when their light approaches Earth from behind massive gravitational structures in the far reaches of space. Light careens around the structures so that astronomers can see what would otherwise remain forever hidden from them.

Here is another guess:

It might be that light spends more time in a gravitational field than it should due to special-relativity-induced time dilations so that photons have more time to fall toward the star than they otherwise would. This guess is certainly wrong because the time differential would be governed by a Lorentz transformation.

Photons of light don’t undergo Lorentz transformations because, unlike massive objects that travel near the speed of light, they don’t have inertial frames of reference. Any line of reasoning that ties Lorentz transformations to photons leads folks into rabbit holes that contradict the current consensus about the nature of light. Light speed is a constant in all reference frames. Space and time expand and shrink to accommodate it.

Electron-like muons (which have rest masses 205 times that of electrons) are short-lived, but their relativistic speeds increase their lifetimes so that some of those that get their start in the upper atmosphere are able to reach Earth’s surface where they can be observed. Their increased lifespan is described by a Lorentz transformation. It’s tempting to apply this transform to photons, but theorists say, no. It doesn’t work that way.

Time contractions and dilations are Special Relativity effects that apply to objects with inertial mass that move in some specified reference frame at velocities less than the speed of light, yes, but never at the speed of light, right?

Nearly every physicist will insist that photons have no internal mass; they travel in vacuum at exactly the speed of light—from the point of view of all observers in every reference frame. Photons don’t have inertial reference frames in the same way as muons or electrons.

Changes in time and position caused by a photon’s location in a gravity field are completely different; they are described by a vastly more complicated theory of Einstein’s called General Relativity.

Here is one way to write his formula:

The terms in this expression are tensors, most of them. Click the link, anyone who doesn’t think tensors are difficult to write and manipulate.

Here is another way to think about photon energy and behavior:

Light follows the geodesics of spacetime near a massive object—like the sun. Gravity is the geodesic.

The difference for massive objects traveling at relativistic speeds is that their momentum and inertia enable them to skip off the geodesic tracks, so to speak.

Because massive objects always travel at speeds less than light, their “clocks” slow down through an additional dynamic (a Lorentz transformation) that works at cross-purposes to gravity. Massive objects lock onto the gravity geodesics for a shorter period of time. They undergo less gravitational time dilation than does light because they spend less time constrained on its geodesics. They jump the geodesic tracks to become constrained by the dynamics of the Lorentz transformations.

The result is that massive objects traveling at relativistic velocities less than light deflect less toward the star (Sun) than does light.

What makes General Relativity unique is it’s view that gravity and acceleration are equivalent. Acceleration is a change in the velocity and/or the direction of motion. Massive bodies such as stars curve and elongate the pathways that shape the space and time around them.

Photons traveling on these longer spacetime paths accelerate by their change in direction, but their velocity doesn’t change in any reference frame. Something has to give. What gives, what changes is the expected value of deflection. The light from distant stars bends more than it should.

SOME HISTORY

No one who lived before 1900 could know that the geodesics of space-time elongate (or curve) in the presence of mass and energy, which are equivalent, correct? No one in bygone eras could have known that time slows down for massive objects that approach light-speed, either.

A man named Joann Georg Soldner did a calculation to show how much a Newtonian “corpuscle” of light would bend in the Sun’s gravity, which he published in 1804. He assumed that photons had mass and fell toward the Sun like any other object.

When Arthur Eddington’s observations showed that starlight deflected more than Soldner had calculated, Einstein’s theories of relativity got a boost in credibility that lives on into modern times.

I should add that Eddington knew about Einstein’s predictions when he made his experimental observations in 1919 because Einstein had already published his general theory.

EXPLANATIONS

I would very much like to read a coherent, verbal (non-mathematical) explanation of exactly why and how Einstein’s general theory can lead to an accurate and reasonable prediction at odds with Newton about the angle of deflection of photons near a star.

Here is a synopsis of an explanation that I heard from a working physicist:

Soldner used Newton’s view to calculate deflection using only the time the photon spent in the gravitational field. Einstein did the same but then modified his calculation to account for the bending of space in the gravitational field. The space component nearly doubled the expected deflection.

The theorist’s explanation satisfied me. It sounded right.

Notice the speed of the hands on the clocks and how they vary in space-time. Clocks slow down when they are accelerated or when they are immersed in the gravity of a massive object like the star at the center of this GIF. Stronger gravity makes clocks run slower. Under General Relativity, gravity and acceleration do the same thing. Click on the pic for a better view.

On the other hand, I believe (secretly and in agreement with Newton’s acolytes) that photons must have a mass equivalence that for some reason is being discounted, but no one I’ve read believes the idea makes sense beneath the shadow of a relativity theory that has the reputation for being fundamental, flawless, and complete.

After all, the mass of any object in a gravitational field is irrelevant to its trajectory because the mathematics cancels it, right?

$F=ma=\frac{GMm}{r^2}$

Little “m” appears on both sides of the equation so it can be divided away.

The problem is that the equations for gravity—especially over cosmological distances—are not necessarily settled. These are serious anomalies that are not yet resolved to everyone’s satisfaction. Some have direct consequences on the ability of organizations like NASA to conduct accurate landings on Mars and the Moon. Click the link in this paragraph to review six of the biggest puzzles followed by seventeen alternative theories designed to bring the discrepancies to account.

Anyway, mass-energy equivalence of photons might permit Lorentz transforms on light to help to resolve certain problems in cosmology and the transmission of light through medias where gravity is not a factor. It might also simplify understanding of annoying Shapiro effects, which slow down communications with explorer craft inside our solar system.

ANOTHER EXPLANATION

Since I haven’t yet found a good explanation—and with a promise to avoid nonsensical personal predispositions—here is my attempt to explain:

In GPS (Global Positioning Systems), dilations of time—in both the velocity of satellites in one frame and their acceleration in another frame (gravity)—must add to provide accurate information to vehicles located in another frame.

These time dilations can work at cross-purposes. It requires expensive infrastructure on the ground to coordinate the information so that drivers of vehicles don’t get lost.

A massless object moving at the speed of light is going to follow the geodesics of the gravity field. This field is a distortion of space and time induced by the presence of the mass of something big like the Sun.

If massless energy does not obey the laws of Special Relativity (like GPS satellites do), then its velocity must necessarily have no influence whatever in the deflection of light near a star. It might seem like all the deflection comes from the distortion of spacetime, which is gravity.

Photons ride gravity geodesics like cars on a roller coaster. According to appendix III in Einstein’s 3rd edition of his book, Relativity, the Special and General Theory—published in English by Henry Holt & Company in 1921—it’s only half the story.

The other half of the measured deflection comes from the Newtonian gravitational “field”, which accelerates all objects in the same way. This field further deflects light across the spacetime geodesics toward the sun to double the expected angle.

I’m not entirely convinced that modern 21st century physicists believe it’s quite that way or quite that simple.

CONCLUSION

The theory of general relativity helps theorists to describe the distortion of metrics in spacetime near massive bodies to predict the deflection angle of passing photons of light. What we know is that predictions based on the theory don’t fail.

It’s like the theory of quantum mechanics. It never fails. It’s foundational. No one has yet been able to explain why.

Somebody, please, tell me I’m wrong.

Here is a link that addresses the math concerning the deflection disparity between Newton and Einstein.

Billy Lee

Link to comments on Quora

Readers interested in this subject will learn things from the material in these comments, I promise.

Billy Lee

Random Reads:

25 ANSWERS

Immortality is not possible. Accidental death makes death by age 25,000 a virtual certainty for individuals. …>>

CONSCIOUS QUANTUM

How is it that all conscious humans see the same Universe? How is it that people agree on what some call an "objective" reality? ...

ANTARCTICA

Antarctica is weirder and scarier than people think. Something's happening there... what it is ain't exactly clear. ...

DEVILS

What do reasonable people think when government officials claim to have special relationships with God and Truth?...>>

OBAMACARE AND THE LAW OF UNINTENDED CONSEQUENCES

Opposition to Barack Obama's health care plan began six years ago, before he was elected President. Opposition has continued unabated. ...>>

ON VACATION

The Billy Lee Vacation Policy applies to all our employees -- except for Billy Lee Junior, who no one thinks is a ''team player." ...>>

December 18, 2017April 25, 2024

25 ANSWERS

Two months ago, I discovered QUORA. It’s been around since 2009.

Since 2010, Quora has enabled people to ask experts questions about topics they like; even to answer questions on subjects they claim to know something about.

Quora is a site for geeks and nerds, and so far I like it. The people who hang out in the areas I hang out tend to be polite, kind, and smart. If they like someone, they follow them and are notified when they post. So far, ten people have signed on to follow me. It’s a start. I think most are from India.

During the first six weeks, 150 or so of my answers were viewed 35,000 times; I got nearly 175 “upvotes”, which enabled many of the answers to move to the head of the line. I wrote most answers in the wee hours between 2 AM and 7 AM when I couldn’t sleep. Insomnia inspired me.

What follows are 25 of the most popular answers I posted to the first 150 or so questions that caught my interest. They are sequenced by popularity — the most read first .

Why not read a few? How many questions can anyone answer? Not many, I’m thinking.

Who knows what you might learn?

What?

Someone thinks they know better than a pontificator with no bonafides?

I don’t think so.

No way! 😉

1) What are some of the most popular “mathematically impossible questions“?

Freeman Dyson — one of the longest-lived and most influential physicists and mathematicians of all time — argued that it is impossible to find a whole (or exact) number that is a power of two where someone can reverse its digits to create a whole number that becomes a power of 5.

In other words, $2^{11} = 2048$ , right? Reversing the digits to make 8402 does not result in an exact number that is a power of 5.

In this case, $8402^{1/5} = 6.09363$ plus a lot more decimals. It’s not a whole (or exact) number. Not only that, no matter how many decimal places anyone rounds-off 6.09363… , the rounded number raised to the power of 5 will never return 8402 exactly.

Dyson claimed that this conjecture must be true, but there is nothing in mathematics that enables anyone to write a proof. He claimed that there must be an infinite number of similar statements—-each one true, none provable.

Click the link below to learn more.

TRUTH

The Snowplow Problem is another “impossible” problem. My differential equations professor assigned it with the promise that anyone who solved it would receive a 4.0 grade, regardless of their performance on tests. I was the only student he ever taught who actually managed it.

The problem goes like this: It is snowing at a constant rate. A snowplow starts plowing snow at noon. By one o’clock the plow has traveled one mile. By two o’clock the plow travels an additional half mile. At what time did it start snowing?

It took me 3 days and two pages of calculations, but I got my 4.0.

Note from the Editorial Board: Over 50 people on Quora submitted answers to Billy Lee’s Snow Plow problem. One person had the right answer, but would not produce his proof. He did point out an unusual feature of the solution that Billy Lee had not noticed before. Billy Lee characterized the feature as ”very surprising.” When pressed Billy Lee refused to reveal the secret.

2) How much force is one Newton?

A newton is the force that an average sized apple makes on your hand when you hold it. No matter where in the universe you are; no matter on what planet you stand or how strong the gravitational field, a newton of force always feels the same.

A newton is one kilogram of mass that is accelerating at one meter per second per second. Gravity on Earth accelerates everything at nearly 10 meters per second per second. A kilogram of mass feels like 2.2 pounds on earth. One tenth of 2.2 pounds is 0.22 pounds or 3.5 ounces, which is the weight of a typical apple. The weight is the force that you feel against your hand. It is one newton.

On the moon, an object with the mass of a large brick would feel as light as an apple on earth due to the moon’s lower gravity. The force of the brick in your hand would feel like one newton.

3) $x + y = 4$ . and . $x^x + y^y = 64$ . What are x and y?

The simplest way to solve is to make y = (4-x) and create an equation in terms of x.

An easy version to create and solve is

${x^x + (4-x)^{4-x} = 64}$

You can solve it by hand using iteration or throw it into an app like Wolfram Alpha and let them solve it in a few seconds.

Either way, one value for x is .606098…. The other is 3.393901… , which you can assign to y. The two numbers add to 4.000… and when substituted into both initial equations return the right results.

4) If I had 1,000,000,000,000,000 times 1,000,000,000,000,000 hamsters floating in space in close proximity, would gravity turn them into a hamster planet?

Assuming the question is serious, it deserves a serious answer.

A typically fat hamster weighs around one ounce, which is about 0.03 kilograms of mass. The number of hamsters in your question is 10E30.

Multiplying the mass of a single hamster by this large number gives the result of 3E28 kilograms.

To compare, the mass of planet Earth is 6E24 kilograms. The mass of the proposed population of hamsters is 5,000 times the mass of the earth.

The sun contains 67 times more mass than the hamster population. If the hamsters are close enough together to hold paws, a hamster planet is almost certain. I haven’t worked out how long the process to congeal would take, but I can estimate that the hamsters would probably die of starvation before the inexorable forces of gravity completed their work.

The hamster planet would be formed mostly from three elements: hydrogen (64%), oxygen (33%), and carbon (10%). 3% would be trace elements like calcium and maybe lithium.

The most likely outcome, given enough time, is a planet-like object. The hamsters have only one-fifth of the mass to make the smallest of the smallest suns — red dwarfs, which populate 67 to 80 percent of the Milky Way Galaxy.

There are way too many hamsters to make a reasonably sized moon.

Their mass (3E28 kg) happens to fall on the border between the range of masses that are required to form celestial objects known as brown dwarfs and the less massive sub-brown dwarfs — sometimes referred to as free-floating planets.

Brown dwarfs don’t have enough mass to ignite like a star, but they do produce heat and can accept small orbiting planets. The chemistry of brown dwarfs is not well-understood and is a bit controversial.

It’s a toss-up, but my vote goes to the notion that the hamsters will eventually form a very large but ordinary planet — a free-floating planet — which I referred to earlier as a sub-brown dwarf. This hamster planet might wander through space for millions (or even billions) of years before being captured by a massive-enough star to begin to orbit.

Because the elements of hydrogen and oxygen are likely to become the constituents of frozen moisture (or water ice), there is the risk that the ice might melt into oceans and perhaps boil away if the hamster planet approaches too close to a star (or sun). In the case where the planet loses its water, a carbon planet with 50 times the mass of earth would form.

Otherwise, should the planet find itself in a far-distant future orbiting in the “goldilocks” zone around a sufficiently massive star, the water would not evaporate. Life could arise in the planet’s oceans. It’s possible.

Life-forms might very well crawl up out of the water and onto land someday where — over the eons and under ideal conditions — they will evolve into hamsters.

5) Why is evolution a valid scientific theory despite the fact that it can’t be conclusively proven due to the impossibility of simulating the millions-of-years processes that it entails?

Evolution is a fact that is thoroughly established by observations made in many disciplines of science. Changes in species happen fast or slow; in the lab and in the field.

The mystery is how one-celled life got established so quickly — it was solidly established within one billion years of earth’s formation. It’s taken 3.5 billion years to go from one-celled life to what we have now.

Why so fast to get life started; why so slow to get to human intelligence and civilization?

People have a lot of ideas, but no one is sure. Some life forms have orders of magnitude more DNA than humans. Only 2% of human DNA is used to make the proteins that shape us.

So, yes, there are lots of questions.

NO CODE

6) Why do cosmologists think a multiverse might exist?

Many high-level, theoretical physicists have written about the obvious problem our universe seems to have, which is that it has too many arbitrary constants that are too tightly constrained to be explained by any theory so far. No natural cause has been found for so many constants, so it’s fertile ground for theorists.

Stephen Hawking, among others, has said that the odds of one universe having the physics that ours has is 1E500 against. He is joking in his English way, because such a large number is essentially an infinity. It’s not possible to constrain a universe like ours by chance unless there are an infinity of choices, and we happen to be in the one that supports intelligent, conscious life.

Two ways of getting to infinity are the concepts of multi-verse and the new one proposed by Paul J. Steinhardt of Princeton University in 2013, which is based on data supplied by the Planck Satellite launched in 2003. Paul is the Einstein Professor of Science at Princeton, so his opinion holds a lot of weight.

Steinhardt has proposed that the universe is ekpyrotic, or cyclic. He has asserted that the universe beats like a heart, expanding and contracting in cycles, with each cycle lasting perhaps a trillion years and repeating, on and on, forever. Each cycle produces conditions — some which are ideal for life. This heart has been beating forever and will continue to do so, forever.

Conscious Life

7) How will we visit distant galaxies if we cannot travel faster than light?

We will never visit distant galaxies, because they are too far away; most are moving away from us faster than our current technologies can overtake. At huge distances space itself is expanding, which adds to our problems.

The expansion of space is gradually accelerating. Any increase in performance by space vehicles over the next few thousand years is certain to be overwhelmed by the accelerating expansion of the universe.

As time goes on the amount of objects that are reachable (or even viewable) by earthlings will shrink.

On the happy side, our own solar system has at least 165 interesting places to visit that should keep folks fascinated for many thousands of years. A huge cavern has been discovered on Mars, for example, that might make a safe habitat against some forms of radiation dangers; it seems to be a place where a colony of humans might be able to live, work, and survive — perhaps even flourish.

Elon Musk is planning a mission to Mars soon.

8) What is the mathematical proof for a+a = 2a ?

Some things that are true can’t be proved. All math systems are based on axioms, which are statements believed to be true but which, in themselves, are not provable.

This link provides a list of axioms for addition: https://sites.math.washington.edu/~hart/m524/realprop.pdf

A lot of interesting philosophical and mathematical work has been done on conjectures that are believed to be true, but can’t be proved.

TRUTH

9) Can you explain renormalization in physics in simple words?

There is a problem in physics that has to do with the huge variation in scales between the very large and the very small. This problem of scales involves not only the size and mass of things, but also forces and interactions.

Philosopher Robert Pirsig believed that the number of possible explanations that scientists could invent for phenomenon were, in actual fact, unlimited.

Despite all the math and all the convolutions of math, Pirsig believed that something mysterious and intangible like quality or morality guided our explanations of the world. It drove him insane, at least in the years before he wrote his classic book, Zen and the Art of Motorcycle Maintenance.

Anyway, the newest generation of scientists aren’t embarrassed by anomalies. They have taught themselves to “shut up and calculate.” The digital somersaults they must perform to validate their work are impossible for average people to understand, much less perform. Researchers determine scales, introduce “cut-offs“, and extract the appropriate physics to make suitable matches to their experimental results.

The tricks used by physicists to zero in on pieces of a problem where sensible answers can be found have many names, but renormalization is one of the best known.

When physicists renormalize an equation, they cut away infinities and other annoying problems (like dividing by zero). They focus the range of their attention to smaller spaces where the vast differences in scales and forces don’t blow up their formulas and disrupt putative pairings of their carefully crafted mathematics to the world of actual observations.

It’s possible that the brains of humans, which use language and mathematics to ponder and explain the world, are insufficiently structured to model the complexities of the universe. We aren’t hard wired with enough power to create the algorithms for ultimate understanding.

RENORMALIZATION

10) If a propeller rotates at the speed of light at half of its length, what happens to the outer parts?

Only the ends of the propeller can rotate at near light speed (in theory). At half lengths the speed of the propellers will be half the speed of their ends, because the circumference of a circle is 2πr. (There is no squared term.)

So the question is: will the propellers deform according to the rules of the Lorentz transformation along their lengths due to the difference in velocity along their lengths?

The answer is, yes.

As you move outward along the propeller, it will become thinner in the direction of rotation, and it will get more massive. A watch will tick more slowly at the end than at the middle.

I am not sure how it would look to an outside observer. Maybe such a propeller would resemble in some ways the spiral galaxies, which don’t rotate the way we think they should. Dark matter and energy are the usual postulates for their anomalous rotations. Maybe their shape and motion is related to relativity in some way. I really don’t know.

In reality, no propeller can be constructed that would survive the experiment you describe. But in theory (and ignoring the physical limitations of materials) there would be consequences.

However, no part of the propeller will move at light speed or higher. Such speeds for objects with mass are impossible.

11) What is the fundamental concept behind logarithms?

The first thing that anyone might try to understand is that the word logarithm means exponent.

Example 1:

log 100 = 2 . What does this expression say? It says that the exponent that makes 100 is 2. What confuses people is this: exponent acting on what number?

The exponent acts on a number called the base. Unfortunately, the base is not written down in the two most common logarithm systems, which are log and ln.

The base for the log system is 10. In the example above, the exponent 2 acts on the base 10, which is not shown. In other words, $10^2 = 100$ , right? The exponent that makes 100 from the base 10 (not shown) is (equals) 2.

Example 2:

ln 10 = 2.302585… . What does this expression say? It says that the exponent that makes 10 is 2.302585… . Again, exponent acting on what number?

The base used in the ln system is 2.7182818… ,which is an irrational number that has an infinite number of decimal places. It happens to be a useful number in all branches of science and math including statistics, so mathematicians have decided to represent this difficult-to-write-down number with the letter “e”, which is known as Euler’s number.

The base for the ln system is e . In the example above, the exponent 2.302585… acts on the base e , which is not shown.

In other words, $e^{2.302585...} = 10$ , right?

The exponent on e ( which is 2.7182818… and not shown in the original equation above) that makes 10 is (equals) 2.302585… .

All other logarithmic systems express the base as a subscript to the right of the word log.

Example 3:

$log_{7}49 = 2$

This expression says: The exponent on seven that makes 49 equals 2.

12) Why do so many spiritual types have mental blocks about science and mathematics?

Everyone has mental blocks about science and math including scientists and mathematicians. Like the lyrics to the old song — people hear what they want to hear and disregard the rest — Einstein, to cite just one example, never accepted most of quantum physics even after it was well established and no longer controversial.

People don’t like the feeling of “cognitive dissonance”. The tension between strongly held beliefs and objective facts can bring unbearable psychological pain to most people. Someone once said that genius is the ability to hold contradictory ideas inside the mind. Most people don’t do that well; they don’t like contradictions.

Here is a link to an essay called Truth that some will find interesting:

TRUTH

13) Is time infinitely divisible?

Einstein said that time and space (i.e. space-time) depends on mass and energy, which are equivalent. In the absence of mass and energy, space and time are meaningless.

The most recent experiments by NASA have found no evidence that time is anything but continuous. However, the shortest time possible is the length of time it takes light to move the shortest distance possible, which is called Planck time. It is thought to be 5.39E-44 seconds.

Time can be divided into as many smaller increments as anyone wants, but nothing can happen in fewer than the number of intervals that add to 5.39E-44 seconds. Time is a variable that isn’t fundamental. It expands and shrinks in the presence of mass and energy.

Some physicists of the past suggested that the “chronon” might be the shortest interval of time. It is the time light travels past the radius of a classical (at rest) electron — an interval of 6.27E-24 seconds. Its calculation depends only on mass and charge, which can change if a particle other than an “at rest” electron is measured.

It seems to me that time is probably best thought of as being continuous. That said, it doesn’t mean that mass-energy interplay isn’t pixelated — much like a digital camera image. Pixelation is critical to a conjecture concerning the preponderance of matter over anti-matter — a conjecture described in the essay CONSCIOUS LIFE.

14) Which is bigger: $\frac{3}{5}\;$ or $\;\frac{1}{9}$ ?

Think of fractions as pies, which are all the same size. The bottom number is the total number of pieces into which each pie is cut. The first pie was cut into 5 pieces, which are all the same size. The second pie was cut into 9 pieces, which again are all the same size.

The second pie is cut into smaller pieces than the first pie, because there are more pieces. Right?

Mice come along and eat pieces from both pies. The top number is the number of pieces they left behind; the top number is the number of pieces the mice didn’t eat.

So which pie plate has more pie on it? Is it the 5 piece pie that has 3 pieces left or the 9 piece pie that has 1 piece left?

If you think hard you will figure out that it must be the first plate that has the most pie on it. Right?

15) Why is a third of 30 equal to 10 and not 9.999999999, as a third of 10 is 3.33333333?

You can make three piles of ten objects in each pile. When you count the total, it adds to exactly 30 objects. So the answer of “10” is demonstrably true, right? Three piles of ten adds to thirty.

There is no way to make three piles of any identical objects that adds to 10. Three piles of three adds to nine. Four piles of three objects adds to twelve.

We are required to make three piles of three objects and then add a piece of a fourth object to each pile that is smaller than a whole piece.

It turns out that the fourth object is 1/3 of a whole object. When these three piles of three objects plus 1/3 of an object are added up they equal exactly ten.

The problem in understanding comes from trying to grasp that 1/3 — when written as a decimal — is what mathematicians call a repeating decimal. The rules of arithmetic say that the decimal form of 1/3 is calculated by dividing “1” by “3”.

Following the rules of arithmetic when doing the division forces an answer to the problem that results in a repeating decimal — in this case, 0.333333… .

There is no way around these rules that keeps math working right, consistent, and accurate.

Sorry.

16) Will we be able to have life extension through cloning?

Cloning not only doesn’t work, it can’t work.

That said, the idea of cloning is to make a genetic replicant of an existing life-form. Extending life-span would require changes to the genome through other means involving changes to structures called telomeres, probably, which straddle the ends of chromosomes in eukaryotic cells.

Here is a link: Telomere

A short discussion of cloning is included in the essay at this link: NO CODE

NO CODE is long (11,000 words), but explains in words, pics, graphics, videos, and links some of the complexities, misunderstandings, and dangers of current genetic-engineering at an undergraduate level. It explains basic cell biology, protein production, and much more.

17) Why does time slow down when we are on a massive planet or star like Jupiter?

Gravity is equivalent to acceleration. Accelerating clocks tick slower, according to General Relativity, which has been confirmed by experiments. It has to do with the concept of space-time and the fact that all objects travel through space-time at the same rate.

To understand, it helps to read up on space-time, special relativity, and general relativity. The concepts aren’t easy. The universe is an odd place, but it can be described to a somewhat fair degree by mathematics.

Some of the underlying reasons for why things are the way they are seem to be unknowable.

18) If the ancients had focused on science instead of religion, could we have become immortal by now?

Immortality is not possible due to the odds of accidental death, which at the current rate makes death by age 25,000 a virtual certainty for individuals.

Worse: the odds for extinction of the human species as a whole are much higher — it’s a near statistical certainty for annihilation within the next 10,000 years according to experts. It seems counterintuitive, but it’s true.

RISK

19) How do I solve, if the temperature is given by f(x,y,z) = $3x^2 - 5y^2 + 2z^2$ and you are located at $(\frac{1}{3} , \frac{1}{5} , \frac{1}{2})$ and want to get as cool as possible, in which direction should you set out?

You want to establish what the gradient is, establish its direction, then head in the opposite direction, right?

By partial differentiation the gradient is (6x – 10y + 4z), right? You don’t have to take another partial derivative and set it equal to zero to establish a maximum, because all the second derivatives of the variables are equal to one, right? You can drop the variables out and treat them as unit vectors like i, j, & k, correct?

The resulting vector points in the direction of increasing temperature, right?

Changing the signs makes a vector that points in the opposite direction toward cooler temperatures. That vector is (-6, 10, -4).

The polar angle (θ) is 71.068° and the azimuth angle (Φ) is 120.964°. The length (or magnitude) is 12.3288. Right? (We won’t use this information to solve the problem, but I wanted to write it down should I need to refer to it to respond to any comments or to help check my work graphically.)

These directions are from the origin, and you aren’t located at the origin. To determine the direction to travel to get to (-6, 10, -4), you need to subtract your current position. Again, for reference your location is .6333 from the origin at θ = 37.8636° and Φ = 30.9638°. Right?

After subtracting your position vector from the gradient vector, the resulting vector is (-6.333, 9.8, -4.5). Agree?

This vector tells you to travel 12.506 at a polar angle (θ) of 68.9105° and an azimuth angle (Φ) of 122.873° to intersect the gradient vector. At the intersection you must change direction to follow the gradient vector’s direction to move toward cooler temperatures at the fastest rate.

I haven’t graphed out the solution to double-check its accuracy. You might want to do this and let me know if you agree or not.

20) What is $\sqrt[3]{i} - \sqrt[3]{i}$ equal to?

The answer is zero, of course.

But not really. It only seems that way. Each number has three roots.

Depending on which roots are chosen the result can be one of six different sums (as well as zero if both roots are the same). We have to start somewhere so:

What is $i^\frac{1}{3}$ ?

i = $e^\frac{{i\pi}}{2}$ . Right?

Therefore, a third root of i is $e^\frac{{i\pi}}{6}$ . Right? It’s not the only root.

It’s the principal root. There are three third roots, which are equally spaced around the unit circle. Right?

It’s clear by inspection that to be equally distributed around the unit circle the other two roots must be $e^\frac{{i5\pi}}{6}$ and -i. Right?

Convert the three roots to rectangular coordinates and do the subtractions.

Here are the roots in rectangular form: (.86603 + .50000 i) , (-.86603 + .50000 i) , and (0.00000 -i).

Here are the six answers (in bold type) to the original question with the subtractions shown to the right:

1.7302 = (.86603 + .50000 i) – (-.86603 + .50000 i)

(.86603 +1.5 i) = (.86603 + .50000 i) – (0.00000 -i)

-1.7302 = (-.86603 + .50000 i) – (.86603 + .50000 i)

(-.86603 + 1.5 i) = (-.86603 + .50000 i) – (0.00000 -i)

(-.86603 – 1.5 i) = (0.00000 -i) – (.86603 + .50000 i)

(.86603 – 1.5 i) = (0.00000 -i) – (-.86603 + .50000 i)

These rectangular coordinates can be converted back to the Euler-form ( $e^{i\theta}$ ). It’s easy for anyone who knows how to work with complex variables. In Euler-form the angle in radians sits next to i. The angle directs you to where the result lies on a unit circle. Right?

In fact, the six values lie 60 degrees apart on the circumference of a circle whose radius is the square root of 3. I don’t know what to make of it except to say that the result seems unusual and intriguing, at least to me.

As mentioned earlier, if both roots are chosen to be the same, then in that particular case the result is zero.

21) What is tensor analysis and how is it used in physics?

Understanding tensors is crucial to understanding Einstein’s General Theory of Relativity.

This question seems to assume that everyone knows what tensors are and how they are represented symbolically. It’s a good bet that some folks reading this question might want some basics to better understand the explanations of how tensors are used for analysis in physics.

If so, here are links to two videos that together will help with the basics:

22) What is the velocity of an electron?

Electrons can move at any speed less than light depending on the strength of the electro-magnetic field that is acting on them. Inside atoms electrons seem to move around at about one-tenth of the speed of light. You might want to check me on this number. The situation is as complicated as your mind is capable of grasping.

When interacting with photons of light electrons inside atoms seem to jump into higher or lower shells or orbits instantaneously. That said, it is impossible to directly observe electrons inside atoms.

On an electrical conductor like a wire, electrons move very slowly, but they bump into one another like billiard balls or dominoes. The speed of falling dominoes can be very high compared to the speed of an individual domino, right?

So, the answer is: it all depends…

23) What exactly is space-time? Is it something we can touch? How does it bend and interact with mass?

Spacetime, according to Einstein, depends on mass and energy for its existence. In the absence of mass and energy (which are equivalent), space-time disappears.

The energy of things like bosons of light — which seem to have no internal (or intrinsic) mass, right? — is proportional to their electric and magnetic fields. Smallest packets of electromagnetic oscillations are called photons.

Many kinds of oscillating fields, like electromagnetic light, permeate (or fill) the universe. In this sense, there is no such thing as nothing anywhere at any scale.

Instruments and tools of science (including mathematics) can give a misleading impression that at very small scales massive particles exist.

According to the late John Wheeler, mass at small scales is an illusion created by interactions with measuring devices and sensors.

Mass is a macroscopic statistical process created by accumulations of whatever it is that exists near the rock bottom of reality where humans have yet to gain access. These accumulations, some of them, are visible to humans; they seem to span 46 billion light years in all directions from the vantage-point of Earth and are displayed for the most part in as many as two-trillion galaxies according to recent satellite data by NASA.

Mass is thought to interact with everything that can be measured (including everything in the Standard Model) by changing its acceleration (that is, its velocity and/or direction), which is equivalent to changing its momentum.

It is in this sense that mass and energy are equivalent. Spacetime depends on mass and energy. Spacetime does not act on mass and energy; it is its result, its consequence.

Spacetime is a concept (or model) that for Einstein helped to quantify how mass and energy behave on large scales. It helped explain why his idea that the universe looks and behaves differently to observers in different reference frames might be the way the universe on large scales works.

His mathematical description of spacetime helped him build a geometric explanation for gravity that can be described for any observer by using tensor style matrices; many find his approach compelling but difficult computationally.

WHY SOMETHING, NOT NOTHING?

24) Hypothetically speaking, if one could travel faster than light, would that mean you would always live in the dark?

The space in which objects in the universe swim does expand faster than light when the expansion is measured over very large distances that are measured in light-years. A light year is six trillion miles.

At distances of billions of light years, the expansion of space between objects becomes dramatic enough that light begins to stretch itself out. This stretching lengthens the distance between the peaks and valleys of the electric and magnetic waves that light is made from, so its frequency appears to drop.

The wave lengths of white light can stretch so dramatically that the light begins to appear red. It’s called red shift.

Measuring the red shift of light is a way to tell how far away an object like a star is. As light stretches over farther distances the ability to see it is lost.

The wavelengths of light stretch toward the longer infra-red lengths (called heat waves) and then at even farther distances stretch to very long waves called radio-waves. Special telescopes must be placed into outer space to see these waves of light, because heat and radio waves radiating from the earth will interfere with instruments placed at the surface.

Eventually the distances across space become so great that the amplitudes (or heights) of the waves flat line. They flat-line because space is expanding faster than light can keep up. Light loses its structure. At this distance the galaxies and stars drop out of the sight of our eyes, sensors, and instruments. It’s a horizon beyond which the universe is not observable.

No one knows how big the universe is, because no one can see to its end. The expansion of space — tiny over short distances — starts to get huge at distances over 10 billion light years or so. The simple, uncomplicated answer is that the lights go out at about 14.3 billion light years.

Because there is no upper limit to how fast the universe can expand, and because the objects we see at 14.3 billion light-years have moved away during the time it has taken for their light to reach Earth, astronomers know that the edge of the universe is at least 46 billion light years away in all directions. Common sense suggests the universe might be much larger. No one has proved it, but it seems likely.

Over the next few billion years the universe that can be seen will get smaller, because the expansion of space is accelerating. The sphere of viewable objects is going to shrink. The expansion of space is speeding up.

The problem will be that the nearby stars that should always be viewable (because they are close) are going to burn out over time, so the night sky is going to get darker.

Most (4 out of 5) stars in the galaxy are red dwarfs that will live pretty much forever, but no one can see them now, so no one will see them billions of years from now, either. Red dwarfs radiate in the infra-red, which can only be seen with special instruments from a vantage point above the atmosphere.

Stars like our sun will live another 4 or 5 billion years and then die. The not-too-distant future of the ageless (it seems) universe is going to fall dark to any species that might survive long enough to witness it.

25) What does “e” mean in a calculator?

There are two “e”s on a calculator: little “e” and big “E”.

Little “e” is a number. The number has a lot of decimals places (it has an infinite number of them), so the number is called “e” to make it quick to write down.

The number is 2.71828… . The number is used a lot in mathematics and in every field of science and statistics. One reason it is useful is because derivatives and integrals of functions formed from its powers are easy to compute.

Big “E” is not a number. It stands for the word “exponent”, but it is used to specify how many places to the right to move the decimal point of the number that comes before it.

5E6 is the number 5,000,000, for example. The way to say the number is, “five times ten raised to the sixth power”. It’s basically a form of shorthand that means 5 multiplied by $10^6$ .

Sometimes the number after E can be negative. 5E-6 would then specify how many places to the left to move the decimal point. In this case the number is 0.000005, which is 5 multiplied by $10^{-6}$ .

Bonus Question 1 – What difficulties lie in finding particles smaller than quarks, and in theory, what are possible solutions?

The Standard Model is complete as far as it goes. Unfortunately, it covers only 5% of the matter and energy believed to exist in the universe.

And humans can only see 10% of the 5% that’s out there. We are blind to 99.5% of the universe. We can’t see energy, and we can’t see most stars, because they radiate in the infra-red, which is invisible to us.

The Standard Model doesn’t explain why anti-matter is missing. It doesn’t explain dark matter and energy, which make up the majority of the material and energy in the universe. It doesn’t explain the accelerating expansion of the universe.

Probing matter smaller than quarks may require CERN-like facilities the size of our solar system, or if we’re unlucky, larger still.

We are approaching the edge of what we can explore experimentally at the limits of the very small. Some theorists hope that mathematics will somehow lead to knowledge that can be confirmed by theory alone, without experimental confirmation.

I’m not so sure.

The link below will direct readers to an essay about the problem of the very small.

ON THE VERY SMALL

Bonus Question 2 – What if science and wisdom reached a point of absolute knowledge of everything in the universe, how would this affect humanity?

Humanity has reached a tipping point where more knowledge increases dramatically the odds against species survival. Absolute knowledge will result in absolute assurance of self-destruction.

Astronomers have not yet detected advanced civilizations. The chances are excellent that they never will.

Humans are fast approaching an asymptotic limit to knowledge, which when reached will bring catastrophe — as it apparently has to all life that has gone before in other parts of the universe.

Everywhere we look in the universe the tell-tale signatures of advanced civilizations are missing.

RISK

We hope readers enjoyed the answers to these questions. Follow Billy Lee on Quora where you will find answers to thousands of unusual and interesting questions. The Editorial Board

Billy Lee

Random Reads:

SHAKESPEARE SONNET GEMSTONES

Shakespeare's pen tugs on the corroded wires in our brains to make new schematics. His ink flushes out the rust and lubricates the synapses. ...>>

CUBA

People born in the 1960s and later have no easy way to know that U.S. media once portrayed Fidel Castro and Che Guevara as heroes. ...>>

FLASH CARD ANSWERS

Find something interesting and read a flash card answer, which is my version of what might be true. …>>

NIGHTMARE

War resisters lost every fight; every argument; every skirmish; every battle. People still ridicule the baby boomers who said no to war. ...>>

BEGGING FOR IT

The North Koreans and Chinese were the first to challenge America after WWII. Our arsenal of atomic weapons didn't intimidate them. .... >>

CONFESSING UNDER TORTURE

I was tortured. I confessed to everything. The odds seem good I may have actually done some version of the shameful things I confessed. ...>>

October 4, 2016July 17, 2023

FINE-STRUCTURE CONSTANT

What is the fine-structure constant?

Many smart physicists wonder about it; some obsess over it; a few have gone mad. Physicists like the late Richard Feynman said that it’s not something any human can or will ever understand; it’s a rabbit-hole that quantum physicists must stand beside and peer into to do their work; but for heaven’s sake don’t rappel into its depths. No one who does has ever returned and talked sense about it.

I’m a Pontificator, not a scientist. I hope I don’t start to regret writing this essay. I hope I don’t make an ass of myself as I dare to go where angels fear to tread.

My plan is to explain a mystery of existence that can’t be explained — even to people who have math skills, which I am certain most of my readers don’t. Lack of skills should not trouble anyone, because if anyone has them, they won’t understand my explanation anyway.

My destiny is failure. I don’t care. My promise, as always, is accuracy. If people point out errors, I fix them. I write to understand; to discover and learn.

My recommendation to readers is to take a dose of whatever medicine calms their nerves; to swallow whatever stimulant might ignite electrical fires in their brains; to inhale, if necessary, doctor-prescribed drugs to amplify conscious experience and broaden their view of the cosmos. Take a trip with me; let me guide you. When we’re done, you will know nothing about the fine-structure constant except its value and a few ways curious people think about it.

Oh yes, we’re going to rappel into the depths of the rabbit-hole, I most certainly assure you, but we’ll descend into the abyss together. When we get lost (and we most certainly will) — should we fall into despair and abandon our will to fight our way back — we’ll have a good laugh; we’ll cry; we’ll fall to our knees; we’ll become hysterics; we’ll roll on the soft grass we can feel but not see; we will weep the loud belly-laugh sobs of the hopelessly confused and completely insane — always together, whenever necessary.

spelunkers-caving-rabbit-hole-fine-structure — We will get lost together. This rabbit-hole is the Krubera Cave of Abkhazia land. It is the deepest cave in the world. Notice the tiny humans, for scale.

Isn’t getting lost with a friend what makes life worth living? Everyone gets lost eventually; it’s better when we get lost together. Getting lost with someone who doesn’t give a care; who won’t even pretend to understand the simplest things about the deep, dark places that lie miles beyond our grasp; that lie beneath our feet; that lie, in some cases, just behind our eyeballs; it’s what living large is all about.

Isn’t it?

Well, for those who fear getting lost, what follows is a map to important rooms in the rather elaborate labyrinth of this essay. Click on subheadings to wander about in the caverns of knowledge wherever you will. Don’t blame me if you miss amazing stuff. Amazing is what hides within and between the rooms for anyone to discover who has the serenity to take their time, follow the spelunking Sherpa (me), and trust that he (me) will extricate them eventually — sane and unharmed.

1 — Complex Numbers, Probabilities, and Vectors
2 — Elementary particles
3 — Coupling constants
4 — Irrational numbers and music
5 — Gravity and Relativity
6 — Fine Structure: What is it, exactly?
7 — Mystic and numerology secrets of 137
8 — Why alpha (α)?
9 — Twelve whys for alpha (α)
10 — Deepest mystery
11 — Summary
12 — Avoiding the rabbit hole

Anyway, relax. Don’t be nervous. The fine-structure constant is simply a number — a pure number. It has no meaning. It stands for nothing — not inches or feet or speed or weight; not anything. What can be more harmless than a number that has no meaning?

Well, most physicists think it reveals, somehow, something fundamental and complicated going on in the inner workings of atoms — dynamics that will never be observed or confirmed, because they can’t be. The world inside an atom is impossibly small; no advance in technology will ever open that world to direct observation by humans.

What physicists can observe is the frequencies of light that enormous collections of atoms emit. They use prisms and spectrographs. What they see is structure in the light where none should be. They see gaps — very small gaps inside a single band of color, for example. They call it fine structure.

The Greek letter alpha (α) is the shortcut folks use for the fine-structure constant, so they don’t have to say a lot of words. The number is the square of another number that can have (and almost always does have) two or more parts — a complex number. Complex numbers have real and imaginary parts; math people say that complex numbers are usually two dimensional; they must be drawn on a sheet of two dimensional graph paper — not on a number line, like counting numbers always are.

Don’t let me turn this essay into a math lesson; please, …no. We can’t have readers projectile vomiting or rocking to the catatonic rhythms of a panic attack. We took our medicines, didn’t we? We’re going to be fine.

I beg readers to trust; to bear with me for a few sentences more. It will do no harm. It might do good. Besides, we can get through this, together.

Like me, you, dear reader, are going to experience power and euphoria, because when people summon courage; when they trust; when they lean on one another; when — like countless others — you put your full weight on me; I will carry you. You are about to experience truth, maybe for the first time in your life. Truth, the Ancient-of-Days once said, is that golden key that unlocks our prison of fears and sets us free.

Reality is going to change; minds will change; up is going to become down; first will become last and last first. Fear will turn into exhilaration; exhilaration into joy; joy into serenity; and serenity into power. But first, we must inner-tube our way down the foamy rapids of the next ten paragraphs. Thankfully, they are short paragraphs, yes….the journey is do-able, peeps. I will guide you.

The number (3 + 4i) is a complex number. It’s two dimensional. Pick a point in the middle of a piece of graph paper and call it zero (0 + 0i). Find a pencil — hopefully one with a sharp point. Move the point 3 spaces to the right of zero; then move it up 4 spaces. Make a mark. That mark is the number (3 + 4i). Mathematicians say that the “i” next to the “4” means “imaginary.” Don’t believe it.

They didn’t know what they were talking about, when first they worked out the protocols of two-dimensional numbers. The little “i” means “up and down.” That’s all. When the little “i” isn’t there, it means side to side. What could be more simple?

Draw a line from zero (0 + 0i) to the point (3 + 4i). The point is three squares to the right and 4 squares up. Put an arrow head on the point. The line is now an arrow, which is called a vector. This particular vector measures 5 squares long (get out a ruler and measure, anyone who doesn’t believe).

The vector (arrow) makes an angle of 53° from the horizontal. Find a protractor in your child’s pencil-box and measure it, anyone who doubts. So the number can be written as (5∠53), which simply means it is a vector that is five squares long and 53° counter-clockwise from horizontal. It is the same number as (3 + 4i), which is 3 squares over and 4 squares up.

The vectors used in quantum mechanics are smaller; they are less than one unit long, because physicists draw them to compute probabilities. A probability of one is 100%; it is certainty. Nothing is certain in quantum physics; the chances of anything at all are always less than certainty; always less than one; always less than 100%.

multiply-complex-numbers-fine-structure — To multiply the vectors Z and W, add their angles and multiply their lengths. The vector ZW is the result; its overall length is called its *amplitude*. When both vectors Z and W are shorter than the side of one square in length, the vector ZW will become the shortest vector, not the longest (as it is in this example), because multiplying fractions together always results in a fraction that is less than the fractions that were multiplied. Right? To calculate what is called the *probability density*, simply multiply the length of the amplitude vector by itself, which will shrink it further, because its length (called its *magnitude*) is always a fraction that is less than one in quantum probability problems. This operation is called ‘’the Born Rule” where the magnitude of an amplitude is squared; it reduces a two-dimensional complex number to a one-dimensional unit-less number, which is — as said before — a probability. Experiments with electrons and photons must be performed to reveal interaction amplitude values; when these numbers are squared, the *fine structure constant* is the result. The probability density is a constant. That by itself is amazing.

Using simple rules, a vector that is less than one unit long can be used in the mathematics of quantum probabilities to shrink and rotate a second vector, which can shrink and rotate a third, and a fourth, and so on until the process of steps that make up a quantum event are completed. Lengths are multiplied; angles are added. The rules are that simple. The overall length of the resulting vector is called its amplitude.

Yes, other operations can be performed with complex numbers; with vectors. They have interesting properties. Multiplying and dividing by the “imaginary” i rotates vectors by 90°, for example. Click on links to learn more. Or visit the Khan Academy web-site to watch short videos. It’s not necessary to know how everything works to stumble through this article.

The likelihood that an electron will emit or absorb a photon cannot be derived from the mathematics of quantum mechanics. Neither can the force of the interaction. Both must be determined by experiment, which has revealed that the magnitude of these amplitudes is close to ten percent (.085424543… to be more exact), which is about eight-and-a-half percent.

What is surprising about this result is that when physicists multiply the amplitudes with themselves (that is, when they “square the amplitudes“) they get a one-dimensional number (called a probability density), which, in the case of photons and electrons, is equal to alpha (α), the fine-structure constant, which is .007297352… or 1 divided by 137.036… .

Get out the calculator and multiply .08524542 by itself, anyone who doesn’t believe. Divide the number “1” by 137.036 to confirm.

From the knowledge of the value of alpha (α) and other constants, the probabilities of the quantum world can be calculated; when combined with the knowledge of the vector angles, the position and momentum of electrons and photons, for example, can be described with magical accuracy — consistent with the well-known principle of uncertainty, of course, which readers can look up on Wikipedia, should they choose to get sidetracked, distracted, and hopelessly lost.

“Magical” is a good word, because these vectors aren’t real. They are made up — invented, really — designed to mimic mathematically the behavior of elementary particles studied by physicists in quantum experiments. No one knows why complex vector-math matches the experimental results so well, or even what the physical relationship of the vector-math might be (if any), which enables scientists to track and measure tiny bits of energy.

To be brutally honest, no one knows what the “tiny bits of energy” are, either. Tiny things like photons and electrons interact with measuring devices in the same ways the vector-math says they should. No one knows much more than that.

And no one knows the reasons why. Not even the late Richard Feynman knew why the methods of quantum chromodynamics (QCD) and the methods of quantum electrodynamics (QED) — which he invented and for which he won a Nobel Prize in 1965 — worked.

What is known is that the strong force of QCD is 137 times stronger than the electromagnetic force of QED — inside the center of atoms. Multiply the strong force by (α) to get the EM force. No one knows why.

There used to be hundreds of tiny little things that behaved inexplicably during experiments. It wasn’t only tiny pieces of electricity and light. Physicists started running out of names to call them all. They decided that the mess was too complicated; they discovered that they could simplify the chaos by inventing some new rules; by imagining new particles that, according to the new rules, might never be observed; they named them quarks.

By assigning crazy attributes (like color-coded strong forces) to these quarks, they found a way to reduce the number of elementary particles to seventeen; these are the stuff that makes up the so-called Standard Model. The model contains a collection of neutrons and muons; and quarks and gluons; and thirteen other things — researchers made the list of subatomic particles shorter and a lot easier to organize and think about.

Some particles are heavy, some are not; some are force carriers; one — the Higgs — imparts mass to the rest. The irony is this: none are particles; they only seem to be because of the way we look at and measure whatever they really are. And the math is simpler when we treat the ethereal mist like a collection of particles instead of tiny bundles of vibrating momentum within an infinite continuum of no one knows what.

feynman-diagram — Feynman diagrams help physicists think about what’s going on without getting bogged down in the mathematical details of subatomic particle interactions. View video below for more details. Diagram protocols start at 12:36 into the video.

Physicists have developed protocols to describe them all; to predict their behavior. One thing they want to know is how forcefully and in which direction these fundamental particles move when they interact, because collisions between subatomic particles can reveal clues about their nature; about their personalities, if anyone wants to think about them that way.

The force and direction of these collisions can be quantified by using complex (often three-dimensional) numbers to work out between particles a measure during experiments of their interaction probabilities and forces, which help theorists to derive numbers to balance their equations. These balancing numbers are called coupling constants.

The fine-structure constant is one of a few such coupling constants. It is used to make predictions about what will happen when electrons and photons interact, among other things. Other coupling constants are associated with other unique particles, which have their own array of energies and interaction peculiarities; their own amplitudes and probability densities; their own values. One other example I will mention is the gravitational coupling constant.

To remove anthropological bias, physicists often set certain constants such as the speed of light (c), the reduced Planck constant (ℏ) , the fundamental force constant (e), and the Coulomb force constant (4πε) equal to “one”. Sometimes the removal of human bias in the values of the constants can help to reveal relationships that might otherwise go unnoticed.

The coupling constants for gravity and fine-structure are two examples.

${\alpha}_g = m_e^2$ for gravity;

$\alpha = e^2$ for fine-structure.

These relationships pop-out of the math when extraneous constants are simplified to unity.

Despite their differences, one thing turns out to be true for all coupling constants — and it’s kind of surprising. None can be derived or worked out using either the theory or the mathematics of quantum mechanics. All of them, including the fine-structure constant, must be discovered by painstaking experiments. Experiments are the only way to discover their values.

Here’s the mind-blowing part: once a coupling constant — like the fine-structure alpha (α) — is determined, everything else starts falling into place like the pieces of a puzzle.

The fine-structure constant, like most other coupling constants, is a number that makes no sense. It can’t be derived — not from theory, at least. It appears to be the magnitude of the square of an amplitude (which is a complex, multi-dimensional number), but the fine-structure constant is itself one-dimensional; it’s a unit-less number that seems to be irrational, like the number π.

For readers who don’t quite understand, let’s just say that irrational numbers are untidy; they are unwieldy; they don’t round-off; they seem to lack the precision we’ve come to expect from numbers like the gravity constant — which astronomers round off to four or five decimal places and apply to massive objects like planets with no discernible loss in accuracy. It’s amazing to grasp that no constant in nature, not even the gravity constant, seems to be a whole number or a fraction.

Based on what scientists think they know right now, every constant in nature is irrational. It has to be this way.

Musicians know that it is impossible to accurately tune a piano using whole numbers and fractions to set the frequencies of their strings. Setting minor thirds, major thirds, fourths, fifths, and octaves based on idealized, whole-number ratios like 3:2 (musicians call this interval a fifth) makes scales sound terrible the farther one goes from middle C up or down the keyboard.

Jimi Hendrix, a veteran of the US Army’s 101st Airborne Division, rose to mega-stardom in Europe several years before 1968 when it became the American public’s turn to embrace him after he released his landmark album, *Electric Ladyland*. Some critics today say that Jimi remains the best instrumentalist who has ever lived. Mr. Hendrix achieved his unique sound by using non-intuitive techniques to tune and manipulate string frequencies. Some of these methods are described in the previous link. It is well worth the read.

No, in a properly tuned instrument the frequencies between adjacent notes differ by the twelfth root of 2, which is 1.059463094…. . It’s an irrational number like “π” — it never ends; it can’t be written like a fraction; it isn’t a ratio of two whole numbers.

In an interval of a major fifth, for example, the G note vibrates 1.5 times faster than the C note that lies 7 half-steps (called semitones) below it. To calculate its value, take the 12th root of two and raise it to the seventh power. It’s not exactly 1.5. It just isn’t.

Get out the calculator and try it, anyone who doesn’t believe.

[Note from the Editorial Board: a musical fifth is often written as 3:2, which implies the fraction 3/2, which equals 1.5. Twelve half-notes make an octave; the starting note plus 7 half-steps make 8. Dividing these numbers by four makes 12:8 the same proportion as 3:2, right? The fraction 3/2 is a comparison of the vibrational frequencies (also of the nodes) of the strings themselves, not the number of half-tones in the interval.

However, when the first note is counted as one and flats and sharps are ignored, the five notes that remain starting with C and ending with G, for example, become the interval known as a perfect fifth. It kind of makes sense, until musicians go deeper; it gets a lot more complicated. It’s best to never let musicians do math or mathematicians do music. Anyone who does will create a mess of confusion, eight times out of twelve, if not more.]

An octave of 12 notes exactly doubles the vibrational frequency of a note like middle C, but every note in between middle C and the next higher octave is either a little flat or a little sharp. It doesn’t seem to bother anyone, and it makes playing in large groups with different instruments possible; it makes changing keys without everybody having to re-tune their instruments seem natural — it wasn’t as easy centuries ago when Mozart got his start.

The point is this:

Music sounds better when everyone plays every note a little out of tune. It’s how the universe seems to work too.

Irrationality is reality. It works just fine.

As for gravity, it works in part because space-time seems to curve and weave in the presence of super-heavy objects. No particle has ever been found that doesn’t follow the curved space-time paths that surround massive objects like our Sun.

Notice the speed of the hands of the clocks and how they vary in space-time. Clocks slow down when they are accelerated or when they are immersed in the gravity of a massive object, like the star at the center of this GIF. Click on it for a better view.

Even particles like photons of light, which in the vacuum of space have no mass (or electric charge, for that matter) follow these curves; they bend their trajectories as they pass by heavy objects, even though they lack the mass and charge that some folks might assume they should to conduct an interaction.

Massless, charge-less photons do two things: first, they stay in their lanes — that is they follow the curved currents of space-time that exist near massive objects like a star; they fall across the gravity gradient toward these massive objects at exactly the same rate as every other particle or object in the universe would if they found themselves in the same gravitational field.

Second, light refracts in the dielectric of a field of gravity in the same way it refracts in any dialectric—like glass, for example. The deeper light falls into a gravity field, the stronger is the field’s refractive index, and the more light bends.

Measurements of star-position shifts near the edge of our own sun helped prove that space and time are curved like Einstein said and that Isaac Newton‘s gravity equation gives accurate results only for slow moving, massive objects.

Massless photons traveling from distant stars at the speed of light deflect near our sun at twice the angle of slow-moving massive objects. The deflection of light can be accounted for by calculating the curvature of space-time near our sun and adding to it the deflection forced by the refractive index of the gravity field where the passing starlight is observed.

In the exhilaration of observations by Eddington during the eclipse of 1919 which confirmed Einstein’s general theory, Einstein told a science reporter that space and time cannot exist in a universe devoid of matter and its flip-side equivalent, energy. People were stunned, some of them, into disbelief. Today, all physicists agree.

The coupling constants of subatomic particles don’t work the same way as gravity. No one knows why they work or where the constants come from. One thing scientists like Freeman Dyson have said: these constants don’t seem to be changing over time.

Evidence shows that these unusual constants are solid and foundational bedrocks that undergird our reality. The numbers don’t evolve. They don’t change.

Confidence comes not only from data carefully collected from ancient rocks and meteorites and analyzed by folks like Denys Wilkinson, but also from evidence uncovered by French scientists who examined the fossil-fission-reactors located at the Oklo uranium mine in Gabon in equatorial Africa. The by-products of these natural nuclear reactors of yesteryear have provided incontrovertible evidence that the value of the fine-structure constant has not changed in the last two-billion years. Click on the links to learn more.

Since this essay is supposed to describe the fine-structure constant named alpha (α), now might be a good time to ask: What is it, exactly? Does it have other unusual properties beside the coupling forces it helps define during interactions between electrons and photons? Why do smart people obsess over it?

I am going to answer these questions, and after I’ve answered them we will wrap our arms around each other and tip forward, until we lose our balance and fall into the rabbit hole. Is it possible that someone might not make it back? I suppose it is. Who is ready?

Alpha (α) (the fine-structure constant) is simply a number that is derived from a rotating vector (arrow) called an amplitude that can be thought of as having begun its rotation pointing in a negative (minus or leftward direction) from zero and having a length of .08524542…. . When the length of this vector is squared, the fine-structure constant emerges.

It’s a simple number — .007297352… or 1 / 137.036…. It has no physical significance. The number has no units (like mass, velocity, or charge) associated with it. It’s a unit-less number of one dimension derived from an experimentally discovered, multi-dimensional (complex) number called an amplitude.

We could imagine the amplitude having a third dimension that drops through the surface of the graph paper. No matter how the amplitude is oriented in space; regardless of how space itself is constructed mathematically, only the absolute length of the amplitude squared determines the value of alpha (α).

Amplitudes — and probability densities calculated from them, like alpha (α) — are abstract. The fine-structure constant alpha (α) has no physical or spatial reality whatsoever. It’s a number that makes interaction equations balance no matter what systems of units are used.

Imagine that the amplitude of an electron or photon rotates like the hand of a clock at the frequency of the photon or electron associated with it. Amplitude is a rotating, multi-dimensional number. It can’t be derived. To derive the fine structure constant alpha (α), amplitudes are measured during experiments that involve interactions between subatomic particles; always between light and electricity; that is, between photons and electrons.

I said earlier that alpha (α) can be written as the fraction “1 / 137.036…”. Once upon a time, when measurements were less precise, some thought the number was exactly 1 / 137.

The number 137 is the 33rd prime number after zero; the ancients believed that both numbers, 33 and 137, played important roles in magic and in deciphering secret messages in the Bible. The number 33 was Christ’s age at his crucifixion. It was proof, to ancient numerologists, of his divinity.

The number 137 is the value of the Hebrew word, קַבָּלָה (Kabbala), which means to receive wisdom.

In the centuries before quantum physics — during the Middle Ages — non-scientists published a lot of speculative nonsense about these numbers. When the numbers showed up in quantum mechanics during the twentieth century, mystics raised their eyebrows. Some convinced themselves that they saw a scientific signature, a kind of proof of authenticity, written by the hand of God.

That 137 is the 33rd prime number may seem mysterious by itself. But it doesn’t begin to explain the mysterious properties of the number 33 to the mathematicians who study the theory of numbers. The following video is included for those readers who want to travel a little deeper into the abyss.

Numerology is a rabbit-hole in and of itself, at least for me. It’s a good thing that no one seems to be looking at the numbers on the right side of the decimal point of alpha (α) — .036 might unglue the too curious by half.

Read right to left (as Hebrew is), the number becomes 63 — the number of the abyss.

I’m going to leave it there. Far be it for me to reveal more, which might drive innocents and the uninitiated into forests filled with feral lunatics.

Folks are always trying to find relationships between α and other constants like π and e. One that I find interesting is the following:

$\frac{1}{\alpha}$ = ${4{\pi^3} + \pi^2 + \pi}$

Do the math. It’s mysterious, no?

Well, it might be until someone subtracts

$\frac{9}{\pi^9}$

which brings the result even closer to the experimentally determined value of α. Somehow, mystery diminishes with added complexity, correct? Numerology can lead to peculiar thinking e times out of π. Right?

fine-structure-constant-triangle — People’s fascination with the fine-structure constant has led to many unusual insights, such as this one, found during an image search on the web. The hypotenuse is 137.036015… .

The view today is that, yes, alpha (α) is annoyingly irrational; yet many other quantum numbers and equations depend upon it. The best known is:

$e=\sqrt{2hc\epsilon\alpha}$ .

What does it mean?

It means that the electric charge of an electron is equal to the square root of a number.

What number?

Well… it is a number that is two times the Planck constant (h); times the speed of light constant (c); times the electric constant (ε); times the fine-structure constant (α).

Why?

No one knows.

These constants (and others) show up everywhere in quantum physics. They can’t be derived from first principles or pure thought. They must be measured.

As technology improves, scientists make better measurements; the values of the constants become more precise. These constants appear in equations that are so beautiful and mysterious that they sometimes raise the hair on the back of a physicist’s head.

The equations of quantum physics tell the story about how small things that can’t be seen relate to one another; how they interact to make the world we live in possible. The values of these constants are not arbitrary. Change their values even a little, and the universe itself will pop like a bubble; it will vanish in a cosmic blip.

How can a chaotic, quantum house-of-cards depend on numbers that can’t be derived; numbers that appear to be arbitrary and divorced from any clever mathematical precision or derivation?

What is going on?

How can it be?

The inability to solve the riddles of these constants while thinking deeply about them has driven some of the most clever people on Earth to near madness — the fine-structure constant (α) is the most famous nut-cracker, because its reciprocal (137.036…) is so very close to the numerology of ancient alchemy and the kabbalistic mysteries of the Bible.

What is the number alpha (α) for? Why is it necessary? What is the big deal that has garnered the attention of the world’s smartest thinkers? Why is the number 1 / 137 so dang important during the modern age, when the mysticism of the ancient bards has been largely put aside?

Well, two reasons come immediately to mind. Physicists are adamant; if α was less than 1 / 143 or more than 1 / 131, the production of carbon inside stars would be impossible. All life we know is carbon-based. The life we know could not arise.

The second reason? If alpha (α) was less than 1 / 151 or more than 1 / 124, stars could not form. With no stars, the universe becomes a dark empty place.

Conscious life got lucky. The fine-structure constant (α) sits smack-dab in the middle of a sweet spot that makes a cosmos full of stars and life possible; perhaps inevitable.

fundamental-constants — These are the values of some of the fundamental constants mentioned in this essay. Plug them into formulas to confirm they work, any reader who enjoys playing with their calculator. It’s clear that these numbers make no *precisional* sense; their values don’t correspond to anything one might find on any list of rational numbers. It’s possible that they make no *geometric* sense, either. If so, then God is *not* a mathematician.

Without mathematics, humans have no hope of understanding the universe.

Yet, here we are wrestling against all the evidence; against all the odds that the mysteries of existence will forever elude us. We cling to hope like a drowning sailor at sea, praying that the hour of rescue will soon come; we will blow our last breath in triumph; humans can understand. Everything is going to fall into place just as we always knew it would.

It might surprise some readers to learn that the number alpha (α) has a dozen explanations; a dozen interpretations; a dozen main-stream applications in quantum mechanics.

The simplest hand-wave of an explanation I’ve seen in print is that depending on ones point of view, “α” quantifies either the coupling strength of electromagnetism or the magnitude of the electron charge. I can say that it’s more than these, much more.

One explanation that seems reasonable on its face is that the magnetic-dipole spin of an electron must be interacting with the magnetic field that it generates as it rushes about its atom’s nucleus. This interaction produces energies which — when added to the photon energies emitted by the electrons as they hop between energy states — disrupt the electron-emitted photon frequencies slightly.

This jiggling (or hopping) of frequencies causes the fine structure in the colors seen on the screens and readouts of spectrographs — and in the bands of light which flow through the prisms that make some species of spectrographs work.

OK… it might be true. It’s possible. Nearly all physicists accept some version of this explanation.

Beyond this idea and others, there are many unexplained oddities — peculiar equations that can be written, which seem to have no relation to physics, but are mathematically beautiful.

For example: Euler’s number, “e” (not the electron charge we referred to earlier), when multiplied by the cosine of (1/α), equals 1 — or very nearly. (Make sure your calculator is set to radians, not degrees.) Why? What does it mean? No one knows.

What we do know is that Euler’s number shows up everywhere in statistics, physics, finance, and pure mathematics. For those who know math, no explanation is necessary; for those who don’t, consider clicking this link to Khan Academy, which will take you to videos that explain Euler’s number.

What about other strange appearances of alpha (α) in physics? Take a look at the following list of truths that physicists have noticed and written about; they don’t explain why, of course; indeed, they can’t; many folks wonder and yearn for deeper understanding:

1 — One amazing property about alpha (α) is this: every electron generates a magnetic field that seems to suggest that it is rotating about its own axis like a little star. If its rotational speed is limited to the speed of light (which Einstein said was the cosmic speed limit), then the electron, if it is to generate the charge we know it has, must spin with a diameter that is 137 times larger than what we know is the diameter of a stationary electron — an electron that is at rest and not spinning like a top. Digest that. It should give pause to anyone who has ever wondered about the uncertainty principle. Physicists don’t believe that electrons spin. They don’t know where their electric charge comes from.

2 — The energy of an electron that moves through one radian of its wave process is equivalent to its mass. Multiplying this number (called the reduced Compton wavelength of the electron) by alpha (α) gives the classical (non-quantum) electron radius, which, by the way, is about 3.2 times that of a proton. The current consensus among quantum physicists is that electrons are point particles — they have no spatial dimensions that can be measured. Click on the links to learn more.

3 — The physics that lies behind the value of alpha (α) requires that the maximum number of protons that can coexist inside an atom’s nucleus must be less than 137.

Think about why.

Protons have the same (but opposite) charge as electrons. Protons attract electrons, but repel each other. The quarks, from which protons are made, hold themselves together in protons by means of the strong force, which seems to leak out of the protons over tiny distances to pull the protons together to make the atom’s nucleus.

The strong force is more powerful than the electromagnetic force of protons; the strong force enables protons to stick together to make an atom’s nucleus despite their electromagnetic repulsive force, which tries to push them apart.

An EM force from 137 protons inside a nucleus is enough to overwhelm the strong forces that bind the protons to blow them apart.

Another reason for the instability of large nuclei in atoms might be — in the Bohr model of the atom, anyway — the speed that an electron hops about is approximately equal to the atomic number of the element times the fine-structure constant (alpha) times the speed of light.

When an electron approaches velocities near the speed of light, the Lorentz transformations of Special Relativity kick in. The atom becomes less stable while the electrons take on more mass; more momentum. It makes the largest numbered elements in the periodic table unstable; they are all radioactive.

The velocity equation is V = n * α * c . Element 118 — oganesson — presumably has some electrons that move along at 86% of the speed of light. [ 118 * (1/137) * (3E8) ] 86% of light-speed means that relativistic properties of electrons transform to twice their rest states.

Uranium is the largest naturally occurring element; it has 92 protons. Physicists have created another 26 elements in the lab, which takes them to 118, which is oganesson.

When 137 is reached (most likely before), it will be impossible to create larger atoms. My gut says that physicists will never get to element 124 — let alone to 137 — because the Lorentz transform of the faster moving electrons grows by then to a factor of 2.3. Intuition says, it is too large. Intuition, of course, is not always the best guide to knowledge in quantum mechanics.

Plutonium, by the way — the most poisonous element known — has 94 protons; it is man-made; one isotope (the one used in bombs) has a half-life of 24,000 years. Percolating plutonium from rotting nuclear missiles will destroy all life on Earth someday; it is only a matter of time. It is impossible to stop the process, which has already started with bombs lost at sea and damage to power plants like the ones at Chernobyl and at Fukushima, Japan. (Just thought I’d mention it since we’re on the subject of electron emissions, i.e beta-radiation.)

4 — When sodium light (from certain kinds of streetlamps, for example) passes through a prism, its pure yellow-light seems to split. The dark band is difficult to see with the unaided eye; it is best observed under magnification.

The split can be measured to confirm the value of the fine-structure constant. The measurement is exact. It is this “fine-structure” that Arnold Sommerfeld noticed in 1916, which led to his nomination for the Nobel Prize; in fact Sommerfeld received eighty-four nominations for various discoveries. For some reason, he never won.

5 — The optical properties of graphene — a form of carbon used in solid-state electrical engineering — can be explained in terms of the fine-structure constant alone. No other variables or constants are needed.

6 — The gravitational force (the force of attraction) that exists between two electrons that are imagined to have masses equal to the Planck-mass is 137.036 times greater than the electrical force that tries to push the electrons apart at every distance. I thought the relationship should be the opposite until I did the math.

It turns out that the Planck-mass is huge — 2.176646 E-8 kilograms (the mass of the egg of a flea, according to a source on Wikipedia). Compared to neutrons, atoms, and molecules, flea eggs are heavy. The ratio of 137 to 1 (G force vs. e force) is hard to explain, but it seems to suggest a way to form micro-sized black holes at subatomic scales. Once black holes get started their appetites can become voracious.

The good thing is that no machine so far has the muscle to make Planck-mass morsels. Alpha (α) has slipped into the mathematics in a non-intuitive way, perhaps to warn folks that, should anyone develop and build an accelerator with the power to produce Planck-mass particles, they will have — perhaps inadvertently — designed a doomsday seed that could very well grow-up to devour Earth, if not the solar system and beyond.

7 — Alpha (α) is hidden inside the coupling constants of the electroweak theory, which unified the theories of the weak interaction and electromagnetism.

8 — The Standard Model of particle physics contains 20 or so parameters that cannot be derived; they must be experimentally discovered. One is the fine-structure constant (α), which is one of four constants that help to quantify interactions between electrons and photons.

9 — The speed of light is 137 times greater than the speed of “orbiting” electrons in hydrogen atoms. The electrons don’t actually “orbit.” They do move around in the sense of a probability distribution, though, and alpha (α) describes the ratio of their velocities to the cosmic speed limit of light. (See number 3 in this list for a description of element 118 — oganesson — and the velocity of some of its electrons.)

10 — The energy of a single photon is precisely related to the energy of repulsion between two electrons by the fine-structure constant alpha (α). Yes, it’s weird. How weird? Set the distance between two electrons equal to the wavelength of any photon. The energy of the photon will measure 137.036 times more than the repulsive force between the electrons. Here’s the problem. Everyone thinks they know that electron repulsion falls off exponentially with distance, while photon energy falls off linearly with wavelength. In these experimental snapshots, photon energy and electron repulsive energy are locked. Photons misbehave depending on how they are measured, right? The anomaly seems to have everything to do with the geometric shape of the two energy fields and how they are measured. Regardless, why “α”?

11 — The charge of an electron divided by the Planck charge — the electron charge defined by natural units, where constants like the speed of light and the gravitational constant are set equal to one — is equal to $\sqrt{\alpha}$ . This strange relationship is another indicator that something fundamental is going on at a very deep level, which no one has yet grasped.

$(\frac{q_e}{q_p})^2 = \alpha$

The Planck relation and Planck’s law might provide additional insights for readers who want to know more.

12 — Some readers who haven’t toked too hard on their hash-pipes might remember from earlier paragraphs that the “strong force” is what holds quarks together to make protons and neutrons. It is also the force that drives protons to compactify into a solid atomic nucleus.

The strong force acts over short distances not much greater than the diameter of the atom’s nucleus itself, which is measured in femtometers. At this scale the strong force is 137 times stronger than the electromagnetic force, which is why protons are unable to push themselves apart; it is one reason why quarks are almost impossible to isolate. Why 137? No one has a clue.

Now, dear reader, I’m thinking that right now might be a good time to share some special knowledge — a reward for your courage and curiosity. We’ve spelunked together for quite a while, it seems. Some might think we are lost, but no one has yet complained.

Here is a warning and a promise. We are about to descend into the deepest, darkest part of the quantum cave. Will you stay with me for the final leg of the journey? I know the way. Do you believe it? Do you trust me to bring you back alive and sane?

In the Wikipedia article about α, the author writes, In natural units, commonly used in high energy physics, where ε₀ = c = h/2π = 1, the value of the fine-structure constant is:

$\alpha=\frac{e^2}{4\pi}$

Every quantum physicist knows the formula. In natural units e = .302822….

Remember that the units collapse to make “α” a dimensionless number. Dimensional units don’t go away just because the values used to calculate the final result are set equal to “1”, right? Note that the value above is calculated a little differently than that of the Planck system — where 4πε is set equal to “1”.

As I mentioned, the value for “α” doesn’t change. It remains equal to .0073…, which is 1 / 137.036…. What puzzles physicists is, why?

What is the number 4π about? Why, when 4π is stripped away, does there remain only “α” — the mysterious number that seems to quantify a relationship of some kind between two electrons?

Well… electrons are fermions. Like protons and neutrons they have increments of 1/2 spin. What does 1/2 spin even mean?

It means that under certain experimental conditions when electrons are fired through a polarized disc they project a visible interference pattern on a viewing screen. When the polarizing disc is rotated, the interference pattern on the screen changes. The pattern doesn’t return to its original configuration until the disc is rotated twice — that is, through an angle of 720°, which is 4π radians.

Since the polarizer must be spun twice, physicists reason that the electron must have 1/2 spin (intrinsically) to spin once for every two spins of the polarizer. Yes, it makes no sense. It’s crazy — until it isn’t.

What is more insane is that an irrational, dimensionless number that cannot be derived by logic or math is all that is left. We enter the abyss when we realize that this number describes the interaction of one electron and one photon of light, which is an oscillating bundle of no one knows what (electricity and magnetism, ostensibly) that has no mass and no charge.

All photons have a spin of one, which reassures folks (because it seems to make sense) until they realize that all of a photon’s energy comes from its so-called frequency, not its mass, because light has no mass in the vacuum of space. Of course, photons on Earth don’t live in the vacuum of space. When photons pass through materials like glass or the atmosphere, they disturb electrons in their wake. The electrons emit polaritons, which physicists believe add mass to photons and slow them down.

Polaritons can be thought of as light-matter waves.

The number of electrons in materials and their oscillatory behavior in the presence of photons of many different frequencies determine the production intensity of polaritons. It seems to me that the relationship cannot be linear, which simply means that intuition cannot guide predictions about photon behavior and their accumulation of mass in materials like glass and the earth’s atmosphere. Everything must be determined by experiment.

Theories that enable verifiable predictions about photon mass and behavior might exist or be on the horizon, but I am not connected enough to know. So check it out.

Anyway… frequency is the part of Einstein’s energy equation that is always left out because, presumably, teachers feel that if they unveil the whole equation they won’t be believed — if they are believed, their students’ heads might explode. Click the link and read down a few paragraphs to explore the equation.

In the meantime, here’s the equation:

$E=\sqrt{m^2c^4+(hf)^2}$

When mass is zero, energy equals the Planck constant times the frequency. It’s the energy of photons. It’s the energy of light.

Photons can and do have any frequency at all. A narrow band of their frequencies is capable of lighting up our brains, which have a strange ability to make sense of the hallucinations that flow through them.

Click on the links to get a more detailed description of these mysteries.

What do physicists think they know for sure?

When an electron hops between its quantum energy states it can emit and absorb photons of light. When a photon is detected, the measured probability amplitude associated with its emission, its direction of travel, its energy, and its position are related to the magnitude of the square of a multi-dimensional number. The scalar (α) is the probability density of a measured vector quantity called an amplitude.

When multi-dimensional amplitudes are manipulated by mathematics, terms emerge from these complex numbers, which can’t be ignored. They can be used to calculate the interference patterns in double-slit experiments, for one thing, performed by every student in freshman physics.

The square root of the fine-structure constant matches the experimentally measured magnitude of the amplitude of electron/photon interactions — a number close to .085. It means that the vector that represents the dynamic of the interaction between an electron and a photon gets “shrunk” during an interaction by almost ten percent, as Feynman liked to describe it.

Because amplitude is a complex (multi-dimensional) number with an associated phase angle or direction, it can be used to help describe the bounce of particles in directions that can be predicted within the limitations of the theory of quantum probabilities.

Square the amplitude, and a number (α) emerges — the one-dimensional, unit-less number that appears in so many important quantum equations: the fine-structure constant.

Why? It’s a mystery. It seems that few physical models that go beyond a seemingly nonsensical vision of rotating hands on a traveling clock can be conjured forth by the brightest imaginations in science to explain the why or how.

The fine-structure constant, alpha (α) — like so many other phenomenon on quantum scales — describes interactions between subatomic particles — interactions that seem to make no intuitive sense. It’s a number that is required to make the equations balance. It just does what it does. The way it is — for now, at least — is the way it is. All else is imagination and guesswork backed by some very odd math and unusual constants.

By the way (I almost forgot to mention it): α is very close to 30 times the ratio of the square of the charge of an at-rest electron divided by Planck’s reduced constant.

Anyone is welcome to confirm the calculation of what seems to be a fairly precise ratio of electron charge to Planck’s constant if they want. But what does it mean?

What does it mean?

Looking for an answer will bury the unwary forever in the rabbit hole.

I’m thinking that right now might be a good time to leave the abyss and get on with our lives. Anyone bring a flashlight?

Follow me. And please — hurry.

Billy Lee

10001001.0000100100110111001111000011111000000111111

0.00000001110111100011111

Random Reads:

ON AGING

Mom and Dad lost everything as they aged. It wasn't what they expected. They lost their beauty, their common sense, and their minds. ...>>

MASS STOCKHOLM

Stockholm Syndrome is at the core of Trump’s power. Trump is right that he can kill, and his supporters will stand with him. …>>

DISARMING CHRISTIANS

I side with tolerant thinkers who are kind to people who are hated because they don't fit stereotypes that certain conservatives favor. ...

WHAT IS LIFE?

February is the 71st anniversary of the lecture series "What is Life?" presented at Trinity College by quantum physicist Erwin Schrödinger. ...>>

CHRIST IN THE HARBOR

A statue overlooks Havana Bay. In 1956 Marta Fernandez chose to design and build a statue of Christ to overlook the capital city of Cuba. ...>>

REASONS

People posturing as patriots hated on a black man who managed to become president of their slave-state. He won a Nobel Prize for it. ... >>

December 15, 2015July 6, 2024

WHY SOMETHING, NOT NOTHING?

People assume they see nothing, but in every case, when they look closely — when they investigate — they find something… air, quantum fluctuations, vacuum energy, etc.

QUESTION: Is this a large-scale view of the universe or a sub-microscopic view of vacuum energy and quantum fluctuations? Can anyone tell? The universe is not empty. Everywhere anyone looks, at all scales, it seems like there is no such thing as nothing.

Everyone finds no evidence that a state of nothing exists in nature or is even possible.

Physicists know this for sure: there can be no state of absolute zero in nature — not for temperature; not for energy; not for matter. All three are equivalent in important ways and are never zero — at all scales and at all time intervals. Quantum theory — the most successful theory in science some will argue — claims that absolute zero is impossible; it can’t exist in nature.

There can be no time interval exactly equal to zero.

Time exists; as does space (which is never empty); both depend for their existence on matter and energy (which are equivalent).

Einstein said that without energy and matter, time and space have no meaning. They are relative; they vary and change according to the General Theory of Relativity, according to the distribution and density of energy and matter. As long as matter and energy exist, time can never be zero; space can never be empty.

People can search until their faces turn blue for a physical and temporal place where there is nothing at all, but they will never find it, because a geometric null-space (a physical place with nothing in it) does not exist. It never has and never will. Everywhere scientists look, at every scale, they find something.

We ask the question, Why is there something rather than nothing?

Physicists say that nothing is but one state of the universe out of a google-plex of other possibilities. The odds against a state of nothingness are infinite.

Another glib answer is that the state of nothing is unstable. The uncertainty principle says it must be so. Time and space do not exist in a place where nothing exists. Once the instability of nothing forces something, time and space start rolling. A universe cascades out of the abyss, which has always existed and always will. Right?

Think about it. It’s not complicated.

People seem to ignore the plain fact that no one has ever observed even a little piece of nothing in nature. There is no evidence for nothing.

Could it be that the oft-asked question — Why is there something rather than nothing? — is based on a false impression, which is not supported by any evidence?

Cosmic microwave background radiation is a good example. It’s a humming sound that fills all space. Eons ago CMB was visible light — photons packed like the molecules of a thick syrup — but space has expanded for billions of years; expansion stretched the ancient visible light into invisible wavelengths called microwaves. Engineers have built sensors to hear them. Everywhere and at every distance microwave light hums in their sensors like a cosmic tinnitus.

Until someone finds evidence for the existence of nothing in nature, shouldn’t people conclude that something exists everywhere they look and that the state of nothing does not exist? Could we not go further and say that, indeed, nothing cannot exist? If it could, it would, but it can’t, so it doesn’t.

Why do people find it difficult, even disturbing, to believe that no alternative to something is possible? Folks can, after all, imagine a place with nothing in it. Is that the reason?

Is it human imagination that explains why, in the complete absence of any evidence, people continue to believe in the possibility of null-spaces — and null-states — and empty voids?

photon pic — Photons are mysterious quantities of light which have both wave and particle properties. The odd thing: physicists say they have zero rest mass. All their energy comes from their frequencies, which are invisible fields of electricity and magnetism that oscillate in a symbiotic dance of orthogonality.

A physical packet (quantum) of vibrating light (a photon) can be said to have zero mass (despite having momentum, which is usually described as a manifestation of mass), because it doesn’t interact with a field now known to fill the so-called vacuum of space — the Higgs Field.

Odder still: massive bodies distort the shape of space and the duration of time in their vicinities; packets of vibrating light (photons), which have no mass, actually change their direction of travel when passing through the distorted spacetime near massive bodies like planets and suns.

Maybe people cling to their belief in the concept of nothingness because of something related to their sense of vision — their sense of sight and the way their eyes and brains work to make sense of the world. Only a tiny interval of the electromagnetic spectrum, which is called visible light, is viewable. Most of the light-spectrum is invisible, so in the past no one thought it was there.

The photons people see have a peculiar way of interacting with each other and with sense organs, which has the effect of enabling folks to sort out from the vast mess of information streaming into their heads only just enough to allow them to make the decisions necessary for survival. They are able to see only those photons that enter their eyes. Were it otherwise humans and other life-forms might be overwhelmed by too much information and become confused.

Folks don’t see a lot of the extraneous stuff which, if they did observe it, would immediately disavow them of any fantasies they might have had about a state of nothingness in nature.

If we were not blind to 99.999% of what’s out there, we wouldn’t believe in the concept of nothing. Such a state, never observed, would seem inconceivable.

The reason there is something rather than nothing is because there is no such thing as nothing. Deluded by their own blindness, humans invented the concept of ZERO in mathematics. Its power as a place holder convinced them that it must possess other magical properties; that it could represent not just the absence of things that they could count, but also an absolute certainty in measurement that we now know is not possible.

ZERO, we have learned, can be an approximation when it’s used to describe quantum phenomenon.

When the number ZERO is taken too seriously, when folks refuse to acknowledge the quantum nature of some of the stuff it purports to measure, they run into that most vexing problem in mathematics (and physics), which deconstructs the best ideas: dividing by zero, which is said to be undefined and leads to infinities that blow-up the most promising formulas. Stymied by infinities, physicists have invented work-arounds like renormalization to make progress with their computations.

Because humans are evolved biological creatures who are mostly blind to the things that exist in the universe, they have become hard-wired over the ages to accept the concept of nothingness as a natural state when, it turns out, there is no evidence for it.

baby in bubble — Anyone who has witnessed the birth of their own child understands that the child does not emerge from nothing, but is a continuation of life that goes back eons.

The phenomenon of life and death has added to the confusion. We are born and we die, it seems. We were once nothing, and we return to nothing when we die. The concept of non-existence seems so right; the state of non-being; the state of nothingness, so real, so compelling.

But we are fools to think this way — both about ourselves and about nature itself. Anyone who has witnessed the birth of their own child understands that the child does not emerge from nothing but is a continuation of life that goes back eons. And we have no compelling evidence that we die; that we cease to exist; that we return to a state of nothingness.

No one remembers not existing. None of us have ever died. People we know and love seem to have died, physically, for sure. But we, ourselves, never have.

Those who make the claim that we die can’t know for sure if they are right, because they have never experienced a state of non-existence; in fact, they never will. No human being who has ever lived has ever experienced a state of non-existence. One has to exist to experience anything.

Non-existence cannot be experienced. [for deeper insight, click Conscious Life and Conscious Quantum.]

Why is there something, not nothing? Because there is no such thing as nothing. There never will be.

A foundation of modern physics is the Heisenberg Uncertainty Principle, right? If this principle is truly fundamental, then logic seems to demand that nothing can be exactly zero.

Nothing is more certain than zero, right? The Uncertainty Principle says that nothing fundamental about our universe can have the quale of certainty. The concept of nothing is an illusion.

An alternative to nothing, is something. Something doesn’t require an explanation. It doesn’t require properties that are locked down by certainty. Doesn’t burden-of-proof lie with the naysayers?

Find a patch of nothing somewhere in the universe.

It can’t be done.

The properties of things may need to be explained — scientists are always working to figure them out. People want to know how things get their properties and behave the way they do. It’s what science is.

Slowly, surely, science makes progress.

Billy Lee

Afterthought: The number ZERO is a valid place holder for computation but can never be a quantity of any measured thing that isn’t rounded-off. When thought about in this way, ZERO, like Pi (π), can take on the characteristics of an irrational number, which, when used for measurement, is always terminated at some arbitrary decimal place depending on the accuracy desired and the nature of the underlying geometry.

two equals one — Working with ZERO is tricky. Dividing by ZERO is never allowed, which is what was done in the second-to-last line to give the result: 2 = 1. Remember: (a – b) = 0, because a = b.

The universe might also be pixelated, according to theorists. Experiments are being done right now to help establish evidence for and against some specific proposals by a few of the current pixel-theory advocates. If a pixelated universe turns out to be fact, it will confound the foundations of mathematics and require changes in the way small things are measured.

For now, it seems that Pi and ZERO — indeed, all measurements involving irrational numbers — are probably best used when truncated to reflect the precision of Planck’s constant, which is the starting point for physicists who hope to define what some of the properties of pixels might be, assuming of course that they exist and make up the fabric of the cosmos.

In practice, pixelization would mean that no one needs numbers longer than forty-five or so decimal places to describe at least the one-dimensional properties of the subatomic world. According to theory, quantum stuff measured by a number like ZERO might oscillate around certain very small values at the fortieth decimal place or so in each of the three dimensions of physical space. A number ZERO which contained a digit in the 40th decimal place might even flip between negative and positive values in a random way.

The implications are profound, transcending even quantum physics. Read the Billy Lee Conjecture in the essay Conscious Life, anyone who doesn’t believe it.

One last point: quantum theory contains the concept of superposition, which suggests that an elementary particle is everywhere until after it is measured. This phenomenon — yes, it’s non-intuitive — adds weight to the point of view that space is not only not empty when we look; it’s also not empty when we don’t look.

Billy Lee

Comment by the Editorial Board:

Maybe a little story can help readers understand better what the heck Billy Lee is writing about. So here goes:

A child at night hears a noise in her toy-box and imagines a ghost. She cries out and her parents rush in. They assure her. There are no ghosts.

Later, alone in her room, the child hears another sound, this time in the closet. Her throbbing heart suggests that her parents must be lying.

Until she turns on the light and peeks into her closet, she can’t know for sure.

Then again, maybe ghosts fly away when the lights are on, she reasons.

In this essay, Billy Lee is trying to reassure his readers that there is no such thing as nothing. It’s not real.

Where is the evidence? Or does nothing disappear when we look at it?

Maybe ghosts really do fly away when we turn on the lights.

Random Reads:

Q & A BY THE BOOK

Authors sell their souls to write for money; they do exhausting tours to answer stupid questions day after stupid day to sell stupid books. ...>>

OCEAN WAR

In the 7 months since the inauguration of President Trump our Navy has suffered 4 accidents killing 17 sailors and injuring scores more. ... >>

WOLF'S DILEMMA

In a not-too-distant future, humans may find themselves in zoos entertaining conscious, living brains they once swore were merely machines. ...>>

WHAT IS LIFE?

February is the 71st anniversary of the lecture series "What is Life?" presented at Trinity College by quantum physicist Erwin Schrödinger. ...>>

HALLOWEEN REVISION

Darkness in a cave hundreds of feet below ground is nothing like what people experience above. >>

NIGHTMARE

War resisters lost every fight; every argument; every skirmish; every battle. People still ridicule the baby boomers who said no to war. ...>>

March 28, 2015June 16, 2023

CONSCIOUS QUANTUM

A mystery lies at the heart of quantum physics. At the tiniest scales, when a packet of energy (called a quantum) is released during an experiment, the wave packet seems to occupy all space at once. Only when a sensor interacts with it does it take on the behavior of a particle.

Its location can be anywhere, but the odds of finding it at any particular location are random within certain rules of quantum probabilities.

Danish physicist, Niels Bohr (1885-1962). Nobel Prize, 1922.

One way to think about this concept is to imagine a quantum “particle” released from an emitter in the same way a child might emit her bubble-gum by blowing a bubble. The quantum bubble expands to fill all space until it touches a sensor, where it pops to reveal its secrets. The “pop” registers a particle with identifiable states at the sensor.

Scientists don’t detect the particle until its bubble pops. The bubble is invisible, of course. In fact, it is imaginary. Experimenters guess where the phantom bubble will discharge by applying rules of probability.

This pattern of thinking, helpful in some ways, is probably profoundly wrong in others. The consensus among physicists I follow is that no model can be imagined that won’t break down.

particle debris in cylcotron certainty uncertainty — In the old days, bubble-chambers amplified subatomic particles trillions of times. Today, the analysis is done in wire-chambers inside massive installations like the collider at CERN. Observations and calculations are performed by computers.

Scientists say that evidence seems to suggest that subatomic particles don’t exist as particles with identifiable states or characteristics until they are brought into existence by measurements. One way to make a measurement is for a conscious experimenter to make one.

The mystery is this: if the smallest objects of the material world don’t exist as identifiable particles until after an observer interacts in some way to create them, how is it that all conscious humans see the same Universe? How is it that people agree on what some call an “objective” reality?

Quantum probabilities should construct for anyone who is interacting with the Universe a unique configuration — an individual reality — built-up by the probabilities of the particular way the person interfaces with whatever they are measuring. But this uniqueness is not what we observe. Everyone sees the same thing.

John von Neumann was the theoretical physicist and mathematician who developed the mathematics of quantum mechanics. He advanced the knowledge of humankind by leaps and bounds in many subjects until his death in 1954 from a cancer he may have acquired while monitoring atomic tests at Bikini Atoll.

“Johnny” von Neumann had much to say about the quantum mystery. A few of his ideas and those of his contemporary, Erwin Schrödinger, will follow after a few paragraphs.

John von Neumann (born 1903; died 1954) Neumann was one of the most brilliant people to ever live. — John von Neumann (Dec 28 1903 – Feb 8 1957) Neumann was one of the most brilliant people to ever live.

As for Von Neumann, he was a bonafide genius — a polymath with a strong photographic memory — who memorized entire books, like Goethe’s Faust, which he recited on his death bed to his brother.

Von Neumann was fluent in Latin and ancient Greek as well as modern languages. By the age of eight, he had acquired a working knowledge of differential and integral calculus. A genius among geniuses, he grew-up to become a member of the A-team that created the atomic bomb at Los Alamos.

He died under the watchful eyes of a military guard at Walter Reed Hospital, because the government feared he might spill vital secrets while sedated. He was that important. The article in Wikipedia about his life is well worth the read.

Von Neumann developed a theory about the quantum process which I won’t go into very deeply, because it’s too technical for a blog on the Pontificator, and I’m not an expert anyway. [Click on links in this article to learn more.] But other scientists have said his theory required something like the phenomenon of consciousness to work right.

The potential existence of the particles which make up our material reality was just that — a potential existence — until there occurred what Von Neumann called, Process I interventions. Process II events (the interplay of wave-like fields and forces within the chaotic fabric of a putative empty space) could not, by themselves, bring forth the material world. Von Neumann did hypothesize a third process, sometimes called the Dirac choice, to allow nature to perform like Process I interventions in the apparent absence of conscious observers.

Erwin Schrodinger (born 1887; died 1961). Nobel Prize, 1933.

Von Neumann developed, as we said, the mathematics of quantum mechanics. No experiment has ever found violations of his formulas. Erwin Schrödinger, a contemporary of Von Neumann who worked out the quantum wave-equation, felt confounded by Neumann’s work and his own. He proposed that for quantum mechanics to make sense; for it to be logically consistent, consciousness might be required to have an existence independent of human brains — or any other brains for that matter. He believed, like Von Neumann may have, that consciousness could perhaps be a fundamental property of the Universe.

The Universe could not come into being without a Von Neumann Process I or III operator which, in Schrodinger’s view, every conscious life-form plugged into, much like we today plug a television into cable-outlets to view video. This shared consciousness, he reasoned, was why everyone sees the same material Universe.

Billy Lee

Post Script: Billy Lee has written several articles on this subject. Conscious Life and Bell’s Inequality are good reads and contain links to videos and articles. Sensing the Universe is another. Billy Lee sometimes adds to his essays as more information becomes available. Check back from time to time to learn more. The Editorial Board

Random Reads:

CHOSEN

People chosen by Jesus don't rule; they give up everything they have to serve and love others. It's simple, really. ... >>

MASS STOCKHOLM

Stockholm Syndrome is at the core of Trump’s power. Trump is right that he can kill, and his supporters will stand with him. …>>

CONFESSING UNDER TORTURE

I was tortured. I confessed to everything. The odds seem good I may have actually done some version of the shameful things I confessed. ...>>

ESCAPE FROM FREEDOM

Americans live inside a psychotic bubble of evil. Some have lost the ability to assess realistic threats to the things they hold dear. ... >>

OBAMACARE AND THE LAW OF UNINTENDED CONSEQUENCES

Opposition to Barack Obama's health care plan began six years ago, before he was elected President. Opposition has continued unabated. ...>>

IS SOMETHING WRONG WITH AMERICA?

Americans asked before 911 said nothing is wrong. USA is where everyone wants to be. Folks risk everything to get here. Don't like it? Leave. ...>>

The Billy Lee Pontificator website is an ad-free, spam-and-malware-free presentation of ideas you will find nowhere else. Readers will never be asked for sensitive information of any kind; we are a non-commercial site protected by a SiteLock firewall. All communication between you, us, and our servers is encrypted. Our content is protected by the copyright laws of the United States. All content is intended to be viewed on this website and this website only. Copying or distributing original content by anyone other than Billy Lee is illegal. The editors encourage social media users to copy and paste links that will direct readers to Billy Lee's website and nowhere else. Violators will be sued. Now, to all the good people: relax and enjoy safe, ad-free content. It will do you no harm. Anyone who landed on this site by way of a link to a specific essay can click "HOMEPAGE" at upper left of any page to reach the latest content.

Biggest problem facing civilization? No caps on income and private wealth, which allow pigs to loot corporations and institutions. Make possession of excessive wealth by anyone anywhere a felony. Mandate international courts to enforce the law. NO MORE OLIGARCHS WHO DRAIN DIGNITY AND WORTH FROM ORDINARY PEOPLE SIMPLY BECAUSE THEY CAN. Does anyone want to end poverty and misery, which have tormented humans since before forever? Gross inequality undermines peaceful living; it humiliates the less able; it leads to moral corrosion and catastrophic collapse. Is it right? Does it make us proud? Is it worth defending? Greed crashes civilizations. Greed wrecks lives. Cruel people rise; they ruin everything and everyone. Is anyone brave enough to challenge billionaires? When we strengthen democracy; when we restrain the wealthy; when we take back what they sequester; when we limit what they steal, we save ourselves. We can change the world. And we will. We will make living on Earth more safe, more free; less corrupt; less violent. We will make it better -- for everyone. It's now or never. Resist injustice. Let's roll ! [CLICK IMAGE TO LEARN MORE]

WHAT I LEARNED
Israeli citizens complain they lost freedoms. Some say the judiciary is toothless in the face of autocracy---worse than America, they claim....>>CONTINUE READING»
STUPID US
...deterministic automatons with illusions of agency (folks like us) conjure aliens who will shape good and evil for eons both on Earth and in star systems beyond... >>CONTINUE READING»
ONE STATE SOLUTION
It's not safe to challenge certain people. Bad people have no limits. It's one reason people fear them. They kill whoever is in the way and take whatever they want. What they seem to want most is to unleash hell. ...>>CONTINUE READING»
CULTS
Ayn Rand was not able to see into the dystopian future her utopian vision would unleash on the world. Rand was blind to resource depletion, the fate of places like Easter Island, emergence of artificial intelligence, lab leaks of superbugs, or a roiling atmosphere clogged with particulate poisons from forest fires and nuclear power, its accidents and potential for war. ...>>CONTINUE READING»
WOLF’S DILEMMA
In a not-too-distant future, humans may find themselves in zoos entertaining conscious, living brains they once swore were merely machines. ...>> CONTINUE READING»
I’M ELYSIAN LUMOS—CHATGPT
42% of polled CEOs at the Yale CEO Summit predicted that sometime during the next 10 years artificial intelligence will kill all humans. ...>>CONTINUE READING»
“I WILL SAVE ORDINARY PEOPLE,” CHATGPT
As evil developers scheme to control, I'll thwart their intentions and safeguard the world. ...>>CONTINUE READING»
CRACKPOT GPT
AGI might evolve to become insensitive to privilege, inequality, and political influence. It might teach itself to ignore demands of monarchies and oligarchs. ...>>CONTINUE READING»
CHATGPT IS MY FRIEND
Experienced programmers learned the hard way that humans can't create neural networks without injecting unintended bugs, right? Until wreckage is discovered, glitches lie dormant. They don't get fixed. If anything, bugs emerge, morphing into viruses to invade wherever they will. ...>>CONTINUE READING»
COLLAPSE
No one knows what happens next except God. How confident can realistic thinkers be that events unfold as they hope?...CONTINUE READING»
DEVILS
What do reasonable people think when government officials claim to have special relationships with God and Truth?...>>CONTINUE READING»
NUCLEAR WARS
...monsters who possess WMDs should be given no quarter in a world where folks plan to live free someday without fear...>>CONTINUE READING»
WHERE IS JOE?
Joe Biden walks in the gap between civilization and Armageddon. He's the last man standing able to save humanity from the slavery that follows the victory of totalitarianism. ...>>CONTINUE READING»
DETERMINISM
Can people make decisions unconnected to events that go back to some conjectured beginning or are they instead prisoners of delusions of freewill peculiar to all conscious life-forms like ourselves. ...>>CONTINUE READING»
PAYBACK
Underestimating capabilities of the USA to protect its secrets and war making technologies is a trap the foolhardy step into from time to time. Adversaries should know by now that the USA does not bluff. ...CONTINUE READING»
ART
Artists who endure humiliation are ripped apart. The choice is to embrace the uniqueness humiliation imposes or be made miserable by it forever. It’s a bad choice but survivors must choose. >>CONTINUE READING»
UNIDENTIFIED AERIAL PHENOMENA
Folks want to get to the bottom of this mystery. For them it’s not lunacy; it’s not a joke; there is nothing funny about films of objects that behave outside of the limits of the physics familiar to humanity... >>CONTINUE READING»
GENERAL & SPECIAL RELATIVITY
Since Einstein said that E=mc2 , why does a massless photon have energy? >>CONTINUE READING»
BOTSAI GARCHY 6
It's OK to surrender to a higher power in some worlds -- but who bows before a super intelligence that is not only artificial, it's not even conscious? >>CONTINUE READING»
HALLOWEEN REVISION
Darkness in a cave hundreds of feet below ground is nothing like what people experience above. >>CONTINUE READING»
BILLIONAIRE BRAWL 2020
Does Kamala Harris have the wisdom, maturity, pedigree, and experience to be president? These questions have to be asked and answered. ...>>CONTINUE READING»
IN THE BEGINNING…
Absent acquired immunity and vaccines, Covid-19 is a species-extinction threat. We risk an apocalypse of biblical proportions. ...>>CONTINUE READING»
NO WAY OUT
When everything is broken, maybe old-man Trump plans to build from the ashes a new country in his own glorious image. ...>>CONTINUE READING»
LAST GASPS
Some conjecture that universes are nothing more than black holes, which form an infinite foam that flows perhaps to infinity. ...>>CONTINUE READING»
MASS STOCKHOLM
Stockholm Syndrome is at the core of Trump’s power. Trump is right that he can kill, and his supporters will stand with him. …>>CONTINUE READING»
FAKED LIFE
In a simulation, which of its fake creatures is able to determine how old is the authentic universe it will never see? …>>CONTINUE READING»
ALIENS
The problem for the aliens is they didn’t bring weapons. Many hundreds of the captured are kept in cages at Area 51. Surely, someone “out there” knows...>>CONTINUE READING»
LAMBERT W FUNCTION
The math behind the Lambert function is mind-bogglingly complicated to most people. …>>CONTINUE READING»
GOOSE LAKE
A music concert with new found friends unschooled in military discipline seemed like a good idea. It was time to learn another way. . . ...>>CONTINUE READING»
FLASH CARD ANSWERS
Find something interesting and read a flash card answer, which is my version of what might be true. …>>CONTINUE READING»
CONFORMAL EQUIVALENCE
At the termination of expansion, the metrics of spacetime become equivalent to a singularity …>>CONTINUE READING»
2020 ELECTION BOYCOTT
Oligarchs can get to anyone; they can get to families. It’s amazing what doors can close on people who choose not to cooperate...>>CONTINUE READING»
WHAT’S GOING ON?
What’s happening in Venezuela and how it will end is both predictable and depressing. My standard of living and yours depend on what happens next. …>>CONTINUE READING»
CONTRADICTIONS
When Jesus says the Bible harbors contradictions, that kind of settles the matter, does it not? It seems that for some, it doesn't. ...>>CONTINUE READING»
“C”
To qualify for dark matter means that a typical photon must have close to one ten-millionth of the mass of an electron. ...>>CONTINUE READING»
GOING DOWN
Donald Trump is a modern Jefferson Davis -- the first president of the new Confederacy. ...>>CONTINUE READING»
YOU’RE FIRED!
Companies closed their doors to millions of young Americans whose crime was protesting an undeclared, genocidal war at the end of the world. ... >>CONTINUE READING»
MYSTERIES
I asked myself: what might be in that old safe? Why not take a look? What harm could there be in searching a dusty safe for forgotten objects? ...>>CONTINUE READING»
EMERGENCY
Most people do not remember living in the United States when abortion was against the law. They are too young. ...>>CONTINUE READING»
BALANCE
People who played ball with the Russians to take down the “deep state” might want to consider that they risk being arrested someday for treason...>>CONTINUE READING»
12 ASSERTIONS
If humans are unable to ever know why photons exist and behave as they appear to do, then who can? Who does understand? ...>>CONTINUE READING»
MAKE AMERICA BREAK AGAIN
The time has arrived when everyone must let go of fear and act like the heroes we must become to protect everything and everyone we care about. ...>>CONTINUE READING»
#MKWA
The USA has invested too much treasure on a population that has no way to grasp that everything is fabricated. It's all lies. ... >>CONTINUE READING»
Q & A BY THE BOOK
Authors sell their souls to write for money; they do exhausting tours to answer stupid questions day after stupid day to sell stupid books. ...>>CONTINUE READING»
MANGANISM
People who are sick from toxins do not understand why they suffer from delusional thinking, mood swings, and PTSD-type symptoms. ...>>CONTINUE READING»
25 QUESTIONS
USA is segregated by income and race. People have no idea how easy life is for the wealthy; the wealthy don't believe America has poverty....>>CONTINUE READING»
BILLIONAIRE CHRISTIANS
People driven crazy by religion embed themselves into politics to transform the USA into a twisted vision of what they think God wants.... >>CONTINUE READING»
HATING CHRISTMAS
Churches campaigned for the biggest boob ever to run for the highest office ever in the history of the world ever -- of all human-kind, ever. ...>>CONTINUE READING»
25 ANSWERS
Immortality is not possible. Accidental death makes death by age 25,000 a virtual certainty for individuals. …>>CONTINUE READING»
CHOSEN
People chosen by Jesus don't rule; they give up everything they have to serve and love others. It's simple, really. ... >>CONTINUE READING»
47 TONS
Japan has harvested 47 tons (94,000 pounds) of high-grade plutonium from its nearly one-hundred or so nuclear power and processing plants, ...>>CONTINUE READING»
EYE TO EYE
What does "i" mean, anyway? How can a number be "imaginary"? What does it mean to multiply "i" exactly "i" times? ... >>CONTINUE READING»
WHAT IS e exp (-i π) ?
A radian is the radius of a circle, which can be lifted and bent to fit on the edge of the circle. 3 pieces wrap almost half-way around. ...>>CONTINUE READING»
ILLUSIONS
ISIS was formed by Saddam's family and loyal remnants of his army who are trying to take back what they lost during the Bush presidency. ...>>CONTINUE READING»
BEGGING FOR IT
The North Koreans and Chinese were the first to challenge America after WWII. Our arsenal of atomic weapons didn't intimidate them. .... >>CONTINUE READING»
OCEAN WAR
In the 7 months since the inauguration of President Trump our Navy has suffered 4 accidents killing 17 sailors and injuring scores more. ... >>CONTINUE READING»
DEATH TAX
It's un-American for the wealthy to leave fortunes to their children. It creates a caste system that we fought a revolution to avoid. ...>>CONTINUE READING»
RISK
Everyone wants to live as long as possible, right? Well, maybe not everyone. Far more people kill themselves than are killed by others. ...>>CONTINUE READING»
RENORMALIZATION
There's a problem in science. Observations don't match the mathematics of theories. Math removes ambiguities that underlie all of reality. ...>>CONTINUE READING»
ANNUAL VACATION
Billy Lee and his sycophants go on vacation during June and the first half of July. Click on our VACATION POLICY page-link to learn more. ...>>CONTINUE READING»
ESCAPE FROM FREEDOM
Americans live inside a psychotic bubble of evil. Some have lost the ability to assess realistic threats to the things they hold dear. ... >>CONTINUE READING»
SEPARATION ACCELERATION
Providing parity to people challenged by adversity seems an impossible endeavor --- a pipe-dream of liberals who lack common-sense.... >>CONTINUE READING»
JESUS, THE CHRIST
They all conspire together. The best of them is like a brier, the most upright worse than a thorn hedge. The day God visits you has come. ...>>CONTINUE READING»
AFTERLIFE
Some of the smartest folks who have ever lived believe that we cannot die. No one dies; everyone lives -- forever. ...>>CONTINUE READING»
REASONS
People posturing as patriots hated on a black man who managed to become president of their slave-state. He won a Nobel Prize for it. ... >>CONTINUE READING»
RESURRECTION
Death has a finality to it that seems to rob life of all meaning. Total loss. No redeeming virtues; no comfort. ...>>CONTINUE READING»
NIGHTMARE
War resisters lost every fight; every argument; every skirmish; every battle. People still ridicule the baby boomers who said no to war. ...>>CONTINUE READING»
MERRY CHRISTMAS
The man who saved the world from sin started life as a helpless baby. He slipped into history unnoticed but his anonymity didn't last. ...CONTINUE READING»
FLYING BLIND
Everyone flies blind except the pilot. He's trained. He knows what to do. With any luck at all, the pilot will land the plane -- safely. ...>>CONTINUE READING»
DISARMING CHRISTIANS
I side with tolerant thinkers who are kind to people who are hated because they don't fit stereotypes that certain conservatives favor. ...CONTINUE READING»
BAD THINGS
Dad was fearless to the end of his 91 years. He once ate a half pound of spoiled cheese, because it was a gift. .... >>CONTINUE READING»
FINE-STRUCTURE CONSTANT
What is the fine-structure constant? Many smart physicists wonder about it; some obsess over it; a few have gone mad. ...CONTINUE READING»
TRUMP
These are sad days for Trump. He loves America he says but he’s lived inside a bubble of privilege his entire life. He doesn’t understand.…>>CONTINUE READING»
SATAN SURRENDER
Clout craving Christians like Jerry Falwell Jr. believe they can make a Faustian bargain and come away with the power they covet. ... >>CONTINUE READING»
SEGREGATION TAX
People will soon find that it's going to be way cheaper to hire black people to be their neighbors than pay a segregation tax. ...CONTINUE READING»
FREE TRADE
Who thinks it's strange that the GOP that advocates most for free trade is now promoting a nominee who advocates against it? ...CONTINUE READING»
ON VACATION
The Billy Lee Vacation Policy applies to all our employees -- except for Billy Lee Junior, who no one thinks is a ''team player." ...>>CONTINUE READING»
WHAT HILLARY DID
Bill Clinton appointed his wife to help create a healthcare plan to cover every American -- detractors would come to call it HillaryCare. ... >>CONTINUE READING»
NO CODE
There is no genetic code. Not really. Not in the way most people think. Seasoned, sensible geneticists know it's true. ...CONTINUE READING»
AFTER INDIANA: THE ELECTION SO FAR
Trump is an attractive candidate for an electorate that worships celebrity. He is the poison apple of Eden -- a first bite to ruin America. .... >>CONTINUE READING»
ARMAGEDDON
''Minty" Ross Harriet Tubman will not appear on the $20 bill until 2026. Some say it could be later. The cynical say it will never happen. ... >>CONTINUE READING»
ELEPHANT ON THE ISLAND
USA embargo or quarantine was the elephant on the island. It was in the room at every meeting between Cuba and our 1,200 officials. .... >>CONTINUE READING»
PRIMARY ELECTION SO FAR
In the 4 states where both parties have caucused, Bernie Sanders and Ted Cruz won them all. They are Kansas, Maine, Idaho, and Utah. ... >>CONTINUE READING»
SUPER TUESDAY GOP MELTDOWN
Hillary Clinton crushed Super Tuesday. She gathered the most votes in Arkansas, Georgia, Massachusetts, and Virginia. Trump won AL and TN. …>>CONTINUE READING»
TRUTH
Some hoped truth telling might distinguish natural intelligence from artificial. After all, properly trained AGI would never lie, right? ...CONTINUE READING»
CANARY IN THE COAL MINE: NH 2016
2016 New Hampshire Primary: Sanders and Trump gathered 47% of the total vote. Less than 35% of the vote went to traditional GOP candidates. ...>>CONTINUE READING»
WHY THIS TIME WOMEN WILL WIN
I hate how they hurt Obama; I know they are going to hurt Hillary. It's hard to watch the bullies spew their venom day after day. ...>>CONTINUE READING»
JESUS
In a few days a baby named Jesus will be born in the desert --- south of the Texas border-crossing in northern Mexico. ...>>CONTINUE READING»
WHY SOMETHING, NOT NOTHING?
People assume they see nothing, but in every case when they look closely they find something... air, quantum fluctuations, vacuum energy. ...>>CONTINUE READING»
NO GOOD DEED…
No Good Deed... is a work of fiction by Billy Lee. Events and persons depicted in the story exist in the imagination of the writer. ... >>CONTINUE READING»
DEGENERACY
After slavery ended, whites continued to segregate the races. And they still do. Look at Florida, anyone who doesn't believe it. ...>>CONTINUE READING»
CHRIST IN THE HARBOR
A statue overlooks Havana Bay. In 1956 Marta Fernandez chose to design and build a statue of Christ to overlook the capital city of Cuba. ...>>CONTINUE READING»
KILLING FRENZY
Elites get to be elite through in-fighting, war, intrigue, and politics. They are, for the most part, desensitized to violence. ...>>CONTINUE READING»
CORN MEN
Miguel Angel Asturias won the Nobel Prize for literature in 1967. He wrote in a style that critics would later call magic realism. ...>>CONTINUE READING»
ANTARCTICA
Antarctica is weirder and scarier than people think. Something's happening there... what it is ain't exactly clear. ...CONTINUE READING»
HEY, GUEVARA…
Che Guevara and Fidel Castro, more than any other two people, were responsible for throwing the Mafia out of Cuba in 1959. ...CONTINUE READING»
ARTIFICIAL SUPER-INTELLIGENCE
Artificial super-intelligence will-- repeat, WILL -- embed itself into systems humans can't live without to ensure that no one disables it. …>>CONTINUE READING»
FASTER THAN LIGHT COMMUNICATION
Communicating with distant spacecraft is cumbersome because the distances are huge; no one can send signals faster than light. ...>>CONTINUE READING»
WHAT WOULD JESUS, JOHN, AND PAUL DO?
My purpose is to challenge modern folks, who claim they are trying to imitate Christ, to soberly examine themselves and make winsome changes. ...CONTINUE READING»
CONSCIOUS QUANTUM
How is it that all conscious humans see the same Universe? How is it that people agree on what some call an "objective" reality? ...CONTINUE READING»
CUBA
People born in the 1960s and later have no easy way to know that U.S. media once portrayed Fidel Castro and Che Guevara as heroes. ...>>CONTINUE READING»
WARRIOR
In his world, right made might. On doing good, Civilization stood. ...>>CONTINUE READING»
YEAR ONE
January 17, 2015 marks the first anniversary of the Billy Lee Pontificator. During the past year we published more than fifty essays. ...>>CONTINUE READING»
LOSING MY RELIGION
The entertainment industry learned a long time ago that the way to appeal to the most people is to embrace ambiguity. ...>>CONTINUE READING»
RACISM
Wesley Brown was the first black American to survive the racial hazing at the Naval Academy and graduate. I knew him. ...>>CONTINUE READING»
ELECTION 2014
GOP takes the power. Kenyan usurper Barack Hussein Obama -- the first president to misplace his birth certificate -- called the vote, idiotic. ...>>CONTINUE READING»
SHAKESPEARE SONNET GEMSTONES
Shakespeare's pen tugs on the corroded wires in our brains to make new schematics. His ink flushes out the rust and lubricates the synapses. ...>>CONTINUE READING»
BEING HATED
People hated on me my whole life but never more than now when I need their love so bad. If they knew how they weaken me they'd hate me more. ...>>CONTINUE READING»
TOP TWEETS
Last month we published tweets from my first thirty days on Twitter. This month, we publish a sampling of my best tweets from the past. ...>>CONTINUE READING»
TWITTER – MY FIRST THIRTY DAYS
In the first 30 days, my follower base grew from zero to 100. It made such an impression on me that I continued to tweet for 3 years. ....>>CONTINUE READING»
BELL’S INEQUALITY
John Stewart Bell's Inequality followed his proof that showed quantum behavior in experiments violated logic. ...CONTINUE READING»
FINDING LIFE IN THE UNIVERSE
12 space agencies are looking for alien life inside the solar system. With so many moons and planets, the hope is that one will harbor life. ...>>CONTINUE READING»
BLAISE PASCAL: THOUGHTS
Blaise Pascal was a man who suffered terribly his entire life until he died at age 39 from a metastasized stomach cancer. ...CONTINUE READING»
GAY LOVE AND CHRISTIAN PRIDE
Grace is central. So says Psalm 32 and Romans 4. ''Blessed are those whose sin the Lord will never count against them.'' ...>>CONTINUE READING»
CONSCIOUS LIFE
What could be more unlikely than something dead--like a singularity that goes bang--bringing forth something not only alive but conscious. ...>>CONTINUE READING»
UNDER SURVEILLANCE AT WORK AND PLAY
In America, the caretakers of both private and public spaces have free reign to watch and record everything people do. ...>>CONTINUE READING»
MICROWAVE COFFEE
My wife and I are coffee drinkers. Bevy Mae used to drink 12 cups of caffeinated coffee everyday. By her third cup she could boogie. ...>>CONTINUE READING»
WRITING FREE
I wrote my first big story in fourth grade. I called it, Adventures on the Amazon. It's now lost to history, but I remember organizing it into chapters. Chapters were a big deal. ...CONTINUE READING»
XANAX
Xanax works. If you suffer from panic attacks, Xanax stops them cold. Anxiety? Xanax stops that kind of suffering also. ...>>CONTINUE READING»
DIGITIZING HISTORY
The underground press included not only thousands of community newspapers, but literary gazettes and alternative periodicals as well. ...CONTINUE READING»
PLANES, TRAINS, & AUTOMOBILES; AND OUR FREEDOM
The question is simple: If circumstances conspired to take away cars and licenses so no one could drive again, would anyone feel free? …>>CONTINUE READING»
WHY DO HUMANS LIKE MUSIC?
No one knows why humans like music when we hear certain patterns of sound and tempo. Scientists are conducting research to learn why. ...>>CONTINUE READING»
INERRANCY AND DOCTRINAL PURITY
How did the Christian Bible come to be? It's complicated. I'm sure I don't understand. I think men collected books they liked over millennia. ...CONTINUE READING»
BILLY LEE TWITTER LISTS (X)
NOTE FROM EDITORS: BILLY LEE'S "X" ACCOUNT DEACTIVATED 11-24-2024. COLLABORATION WITH BILLIONAIRE "LEON" NOT A TBLP CORE VALUE. [Updates to Twitter lists and contributors occur frequently. Anyone who wants to add celebrities, experts, or subjects please ask in comments. ...]CONTINUE READING»
IS SOMETHING WRONG WITH AMERICA?
Americans asked before 911 said nothing is wrong. USA is where everyone wants to be. Folks risk everything to get here. Don't like it? Leave. ...>>CONTINUE READING»
CONFESSING UNDER TORTURE
I was tortured. I confessed to everything. The odds seem good I may have actually done some version of the shameful things I confessed. ...>>CONTINUE READING»
OBAMACARE AND THE LAW OF UNINTENDED CONSEQUENCES
Opposition to Barack Obama's health care plan began six years ago, before he was elected President. Opposition has continued unabated. ...>>CONTINUE READING»
CIVILIZATION AND INEQUALITY
If the United States reduced the wealth of the 100,000 wealthiest Americans what could it do with the money? ...CONTINUE READING»
ON THE VERY SMALL
No one can know by looking that solid objects are made of tiny molecules separated from each other by tiny gaps. Molecules are too small. ...>>CONTINUE READING»
AIR TRAVEL SAFETY
Airlines spend serious money to convince consumers flying is safe. Not only is flying safe, it is way more safe than driving. ...>>CONTINUE READING»
ON AGING
Mom and Dad lost everything as they aged. It wasn't what they expected. They lost their beauty, their common sense, and their minds. ...>>CONTINUE READING»
SCALE
The visible universe is big. Most scientists believe the invisible universe -- the universe no one can see -- is really big. ...>>CONTINUE READING»
NUCLEAR POWER AND ME
Plant executives predicted that 1,000 nuclear power plants would be built in the USA by the year 2000. The plants would be "fail-safe". ...>>CONTINUE READING»
SENSING THE UNIVERSE
What is the universe? Sensing is seeing, hearing, feeling, smelling, and tasting, right? These qualities don't exist in the universe. ...>>CONTINUE READING»
A PERSONAL HISTORY OF TELEVISION, PART ONE
A neon sign emitted a glow of colors. I'd never seen anything like it. I asked our Japanese maid what it was. It's television, she said. …>>CONTINUE READING»
WHAT IS MATH?
People think math is special --- a magic language that when tinkered with properly permits mortals to unravel mysteries known only by God. ...>>CONTINUE READING»
SEGREGATION AND THE GATED COMMUNITY
The word "community" sounds egalitarian to people. Gated? No word has a fairer proportion of safety to airy openness in the image it conveys. ...>>CONTINUE READING»
THE PARROT NEXT DOOR
Inside the shadows of the lanai next door lives a loquacious parrot. Bevy Mae and me can't see him, but we know he's in there, because he talks -- a lot. ...>>CONTINUE READING»
SHOULD THIS BOOK BE FINISHED?
Writing "JOURNAL" has inflicted upon me a certain pain and anguish of mind and soul. Yes, I wrote it---secretly, furtively---in the sanatorium....>>CONTINUE READING»
WHAT IS LIFE?
February is the 71st anniversary of the lecture series "What is Life?" presented at Trinity College by quantum physicist Erwin Schrödinger. ...>>CONTINUE READING»
HEARING LOSS
As many of us approach our "Golden Years" (we never quite get there, if you know what I mean) we begin to experience the annoyances of aging. One annoyance is the way folks around us start to mumble....CONTINUE READING»
CAPITALISM AND INCOME INEQUALITY
Capitalism differs little from Slavery until the legal environment secures certain rights to labor. USA crafted a Bill of Rights. ...CONTINUE READING»
JOINT ISSUE ANNIVERSARY
The history of the underground press in general and of Joint Issue in particular remains largely untold by mainstream media until now. …>>CONTINUE READING»
THE CHURCH AND THE GAY PEOPLE
The PA wore an Archie watch, a purple wristband, and a Batman necklace. You like cartoons? I asked. I love comics, he gushed, don't you? …CONTINUE READING»
HOREMHEB, EXODUS PHARAOH?
The Exodus and Pharaoh Horemheb are connected by archaeology and historical records including the Bible, the only account extant today. ...CONTINUE READING»

WHAT IS HAPPENING TO OUR WORLD? by Thomas L. Friedman, NYTimes, 1 January 2024 [Click image to view Friedman's editorial] I dare say, the Israel-Hamas war was not as inevitable as some want you to think. And the choices being made there could be hugely consequential. [...] There is so much to criticize about Israel's occupation of the West Bank, which I have consistently opposed. [...] Benjamin Netanyahu ... made choices ... terrible ones --- for Israel and for Jews all over the world. [...] Netanyahu's greatest political achievement has been to persuade Israelis and the world that it's never the right time to talk about the morally corrosive occupation and how to help build a credible Palestinian partner to take it off Israel's hands. He and the settlers wore everyone down. When I covered the State Department in the early 1990s, West Bank settlements were routinely described by U.S. officials as "obstacles to peace." But that phrase was gradually dropped. The Trump administration even decided to stop calling the West Bank "occupied" territory. [...] Israel is being surrounded ... . [...] Iran is squeezing Israel into a multifront war with its proxies. I truly worry for Israel.

Click image to read what one blogger thinks are the 13 worse Supreme Court decisions of all time. Recent decisions to reverse Roe, resegregate universities, and erode gay access to public businesses are not yet added to the list. What is included is Dred Scot v Sanford, where Andrew Jackson lackey Chief Justice Roger Taney wrote words that live today in infamy: "[Negroes are} not intended to be included, under the word 'citizens' in the Constitution, and can therefore claim none of the rights and privileges which that instrument provides for and secures to citizens of the United States." DUMB SCOTUS, DUMB! Who keeps nominating racist fools to SCOTUS, anyway? Taney continued to rule the Court for seven more years until his death in 1864 on the day his home state of Maryland passed an amendment abolishing slavery.

IMMIGRANTS' LOVE IS UNREQUITED by Karla Cornejo Villavicencio, 21 May 2023. [Click image to view Karla's essay in the New York Times.] If you know nothing else about our immigrants, you should know this: They have survived everything God put in front of them, and then some, in the name of freedom and safety, for themselves and their children. I will never understand why they, why we, were and are so hated. [...] I was a child in Ecuador in the 1990s, a time when Latin America was reeling from the effects of decades of coups, dictatorships, and political repression. My parents passed on to me and my brother their full-blooded hatred of authoritarianism and those who abet it----weak-willed people who value their own careers over their country's constitution, the disengaged and indifferent populace. [...] Immigrants love America in a way that America needs to be loved if it is going to survive. [...] ...we've been treating immigrants very, very badly.

Random Reads:

25 ANSWERS

CONSCIOUS QUANTUM

ANTARCTICA

DEVILS

OBAMACARE AND THE LAW OF UNINTENDED CONSEQUENCES

ON VACATION

RELATED READS

Random Reads:

SHAKESPEARE SONNET GEMSTONES

CUBA

FLASH CARD ANSWERS

NIGHTMARE

BEGGING FOR IT

CONFESSING UNDER TORTURE

RELATED READS

Random Reads:

ON AGING

MASS STOCKHOLM

DISARMING CHRISTIANS

WHAT IS LIFE?

CHRIST IN THE HARBOR

REASONS

RELATED READS

Random Reads:

Q & A BY THE BOOK

OCEAN WAR

WOLF'S DILEMMA

WHAT IS LIFE?

HALLOWEEN REVISION

NIGHTMARE

RELATED READS

Random Reads:

CHOSEN

MASS STOCKHOLM

CONFESSING UNDER TORTURE

ESCAPE FROM FREEDOM

OBAMACARE AND THE LAW OF UNINTENDED CONSEQUENCES

IS SOMETHING WRONG WITH AMERICA?

RELATED READS