What is 
?
I posted a long answer on Quora.com where it sort of didn’t do well.
Answers given by others were much shorter but they seemed, at least to me, to lack geometric insights. After two days my answer was ranked as the most read, but for some reason no one upvoted it. It did receive a few positive replies though.
I can’t help but believe that there must be nerds in cyberspace who might enjoy my answer. Why not post it on my blog? Maybe someday one of my grandkids will get interested in math and read it.
Who knows?
Anyway, below is a pic and a working GIF, which should help folks understand better. Anyone who doesn’t understand something can always click on a link for more information.
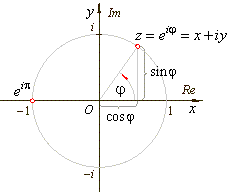
Here is the drawing I added and the answer:
. The point is shown at .2078… on the real number line. An imaginary number raised to the power of an imaginary number yields a result that is a real number. How can that be? It’s something to ponder; something to think about. The Editorial Board What is 
?
The expression evaluates to minus one; the answer is (-1). Why?
Numbers like these are called complex numbers. They are two-dimensional numbers that can be drawn on graph-paper instead of on a one-dimensional number line, like the counting numbers. They are used to analyze wave functions — i.e. phenomenon that are repetitive — like alternating current in the field of electrical engineering, for example.
A simplified explanation of starts at 02:30.
“e” is a number that cannot be written as a fraction (or a ratio of whole numbers). It is an irrational number (like π, for instance). It can be approximated by adding up an arbitrary number of terms in a certain infinite series to reach whatever level of precision one wants. To work with “e” in practical problems, it must be rounded off to some convenient number of decimal places.
Punch “e” into a calculator and it returns the value 2.7182…. The beauty of working with “e” is that derivatives and integrals of functions based on exponential powers of “e” are easy to calculate. Both the integral and the derivative of ex is ex — a happy circumstance that makes the number “e” unusually curious and extraordinarily useful in every discipline where calculus is necessary for analysis.
What is “e” raised to the power of (-iπ) ?
A wonderful feature of the mathematics of complex numbers is that all the values of expressions that involve the number “e” raised to the power of “i” times anything lie on the edge (or perimeter) of a circle of radius 1. This feature makes understanding the expressions easy.
I should mention that any point in the complex plane can be reached by adding a number in front of 
to stretch or shrink the unit circle of values. We aren’t going to go there. In this essay “e” is always preceded by the number “one“, which by convention is never shown.
The number next to the letter “i” is simply the angle in radians where the answer lies on the circle. What is a radian? It’s the radius of the circle, of course, which in a unit circle is always “one”, right?
Wrap that distance around the circle starting at the right and working counter-clockwise to the left. Draw a line from the center of the circle at the angle (the number of radius pieces) specified in the exponent of “e” and it will intersect the circle at the value of the expression. What could be easier?
For the particular question we are struggling to answer, the number in the exponent next to “i” is (-π), correct?
“π radians” is 3.14159… radius pieces — or 180° — right? The minus sign is simply a direction indicator that in this case tells us to move clockwise around the unit circle — instead of counter-clockwise were the sign positive.
After drawing a unit circle on graph paper, place your pencil at (1 + 0i)—located at zero radians (or zero degrees) — and trace 180° clockwise around the circle. Remember that the circle’s radius is one and its center is located at zero, which in two dimensional, complex space is (0 + 0i). You will end up at the value (-1 + 0i) on the opposite side of the circle, which is the answer, by the way.
[Trace the diagram several paragraphs above with your finger if you don’t have graph paper and a pencil. No worries.]
Notice that +π radians takes you to the same place as -π radians, right? Counter clockwise or clockwise, the value you will land on is (-1 + 0i), which is -1. The answer is minus one.
Imagine that the number next to “i” is (π/2) radians (1.57… radius pieces). That’s 90°, agreed? The sign is positive, so trace the circle 90° counter-clockwise. You end at (0 + i), which is straight up. “i” in this case is a distance of one unit upward from the horizontal number line, so write the number as (0 + i) — zero distance in the horizontal direction and “plus one” distance in the “i” (or vertical) direction.
So, the “i” in the exponent of “e” says to “look here” to find the angle where the value of the answer lies on the unit circle; on the other hand, the “i” in the rectangular coordinates of a two-dimensional number like (0 + i) says “look here” to find the vertical distance above or below the horizontal number line.
When evaluating “e” raised to the power of “i” times anything, the angle next to “i”—call it “θ”—can be transformed into rectangular coordinates by using this expression: [cos(θ) + i sin(θ)].
For example: say that the exponent of “e” is i(π/3). (π/3) radians (1.047… radius pieces) wraps around the circumference to 60°, right? The cosine of 60° is 0.5 and the sine of 60° is .866….
So the value of “e” raised to the power of i(π/3) is by substitution (0.5 + .866… i ). It is a two-dimensional number. And it lies on the unit circle.
The bigger the exponent on “e” the more times someone will have to trace around the circle to land at the answer. But they never leave the circle. The result is always found on the circle between 0 and 2π radians (or 0° and 360°) no matter how large the exponent.
It’s why these expressions involving “e” and “i” are ideal for working with repetitive, sinusoidal (wave-like) phenomenon.
In case some readers are still wondering about what radians are, let’s review:
A radian is the radius of a circle, which can be lifted and bent to fit perfectly on the edge of the circle. It takes a little more than three radius pieces (3.14159… to be more precise) to wrap from zero degrees to half-way around any circle of any size. This number — 3.14159… — is the number called “π”. 2π radians are a little bit more than six-and-a-quarter radians (radius pieces), which will completely span the perimeter (or circumference) of a circle.
A radian is about 57.3° of arc. Multiply 3.1416 by 57.3° to see how close to 180° it is. I get 180.01… . The result is really close to 180° considering that both numbers are irrational and rounded off to only a few decimal places.
One of the rules of working with complex numbers is this: multiplying any number by “i” rotates that number by 90°. The number “i” is always located at 90° on the unit circle by definition, right? By the rule, multiplying “i” by “i” rotates it another 90° counter-clockwise, which moves it to 180° on the circle.
180° on the unit circle is the point (-1 + 0i), which is minus one, right?
So yes, absolutely, “i” times “i” is equal to -1. It follows that the square root of minus one must be “i”. Thought of in this way, the square root of a minus one isn’t mysterious.
It is helpful to think of complex numbers as two dimensional numbers with real and imaginary components. There is nothing imaginary, though, about the vertical component of a two-dimensional number.
The people who came up with these numbers thought they were imagining things. The idea that two-dimensional numbers can exist on a plane was too radical at the time for anyone to believe. Numbers, they believed, only existed on a one-dimensional number line of one dimension and no place else.
Of course they were mistaken. Numbers can live in two, three, or even more dimensions. They can be as multi-dimensional as needed to solve whatever the mysteries of mathematical analysis might require.
Click the link, “What is Math?” for another explanation.
Billy Lee