People seem to think that mathematics is something special — a kind of magic language that when tinkered with properly makes it possible for mortals to unravel mysteries about the universe hitherto known only by God.
I see it differently. Mathematics isn’t a language per se. Although mathematics can be (and is) explained by language, math itself is a collection of rules and symbols that makes it possible to avoid the encumbrances, flourishes, and ambiguities of language. It accomplishes this feat by defining things and their relationships in strictly limited — but important — ways.
Math involves symbols and rules that aren’t explained inside the equations. It is the lack of words that gives math its mysterious and magical reputation. But once everything is defined and understood, applying the contrived but logical rules of mathematics enables folks to manipulate equations to uncover previously hidden and non-intuitive relationships among the things they have defined.
What am I saying exactly? I am saying that it is possible to use words alone to describe the process of solving and manipulating an equation, which can lead to insights into the relationship of the things in the equations. But these words will make the process of computation cumbersome, impractical, and confusing.
Spoken language contains noise and nuances that interfere with the manipulation of carefully defined relationships between narrowly defined variables. Yes, the no-nonsense logic and bare bones precision of mathematics as well as the reduction of things to a few carefully chosen attributes enables mathematicians to apply rules to discover consequences that might otherwise remain undiscovered.
But the tightness of mathematical construction makes it a tool which is almost useless for describing and analyzing many subtle yet vivid experiences of a conscious mind — like beauty, the feel of an orgasm, or the experience of grief. For these realities of conscious experience, mathematics has a reputation for being irrelevant.
Spoken language gives conscious humans the messy modeling mechanism they need to connect with each other to share and understand the more nuanced experiences of life. The messiness and ambiguity of spoken language makes the unique intimacies of human communication possible. Mathematics, despite its elegance, doesn’t do intimacy well.
The Euler Identity, illustrated above, is sometimes presented as an example of the mysterious power of mathematics. But if anyone takes the time to think about it, what does the equation say? It says that minus one plus one equals zero.
The explanation is easy. -1 can be rewritten as e raised to the power of i times π because of simple rules, which place on a circle of radius 1 all the values of e raised to the ith power times anything.
The number that sits next to i is the angle in radians where the result lies, right? In this case, an angle of π radians (180°) takes the value 1 (at 0°, or 0 radians) to half-way around the circle to the value -1.
Easy… , right?
Despite the reputation of equations for precision, it turns out that physicists and other scientists struggle to make mathematics match the results of real-world measurements. It has to do with the problem of scales, mostly.
The electrical force is a trillion times a trillion times a trillion times greater than the force of gravity at the scale of electrons and protons. At the scale of quarks, it’s one-hundred-thousand times greater still.
It’s one example.
The non-technical public is unaware for the most part that astronomical observations involving the movement of stars, planets, and other celestial bodies — or the results of observations made of the subatomic world (no matter how carefully contrived) — fail as often as not to provide results sufficiently in agreement with mathematics to be of any practical use until they are massaged a little.
Fudge-factors are a big component of doing real science. People have won Nobel prizes for inventing fudge-factor protocols to fix things.
It’s true.
Renormalization, perturbation theory (for phenomenon both small and large), Green’s functions, propagators, Feynman diagrams, and many other adjustments and tweaks make up the contortions and modifications that scientists overlay onto their beautiful equations to make them work.
They claim to have good reasons for all the tinkering; it’s complicated down there among the quarks or up there, among the quasars; there are nuances and messiness and ambiguity in the underlying reality of nature that no one can see or fully understand — not now; not anytime soon; perhaps not ever.
At subatomic scales, a tangled mess of virtual particles — which come into and out of existence more or less spontaneously — often gets the blame for the mismatch between mathematical elegance and the cold reality of experimental results.
On the scale of the universe, dark matter and energy (which have yet to be detected or observed) are sometimes blamed for anomalies. Click on the link in this paragraph to learn more.
It’s possible that no system involving mathematics can be contrived by humans to bring the satisfaction of knowing everything for certain; nothing we are able to invent will bring a tranquil end to the pain of cognitive dissonance that seems to drive our species to wonder and explore to find the satisfying answer.
On the other hand, perhaps mathematics is more complex and goes further than we know. Methods may yet be discovered to make mathematics and physics match-up with better accuracy and precision.
Recent work by Cohl Furey and others on numbers known as octonions is showing tantalizing hints that internal properties like the force and charge of particles and their external manifestations like mass and spin are connected in peculiar ways that might be described by a more fully developed mathematics.
Dixon algebra (a combination of four division algebras) is a tool that people are using to collaborate in the search for a path forward. So far, success eludes them. Some experts are hopeful, but many express skepticism.
The more deeply people travel into the complexities of mathematics and science the more elusive truth seems to become; perhaps God is not a mathematician; maybe Einstein was right when he said, God does not play at dice.
A die is cast into the lap, yes, but its decision is from the LORD, according to an old proverb of Solomon.
Can it really be true that understanding the world is beyond the limitations of all life on the earth — beyond the abilities of the most brilliant minds that have lived or ever will live?
Is it possible that the universe cannot be understood by any conscious life anywhere in the universe for all time?
If so, it’s time to kneel.
Billy Lee



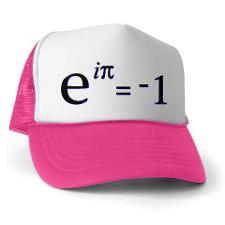


Lovely website interesting and creative… wish i knew my maths!